Question 625772: 2 cos3x = − square root2 , x∈[0,2π ]
solve
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! Solving equations like this usually start with transforming the equation into the form:
TrigFunction(expression) = number
The only thing we need to do to your equation to get it into this form is to get rid of the 2 in front of cos(3x). Dividing both sides of the equation by 2 we get:

Once we have this form we find the general solution. Since Trig functions are periodic, these equations often have an infinite number of solutions. The general solution is a set of equations that express this infinite set of solutions.
We should recognize that  is a special angle value for cos. (So we will not need our calculators for this problem.) We should know that the reference angle for an anglewhose cos is is a special angle value for cos. (So we will not need our calculators for this problem.) We should know that the reference angle for an anglewhose cos is 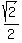 will be will be  . And for the cos to have a negative value, the angle must terminate in the second or third quadrants. Putting these facts together we find that we want the angles that terminate the second and third quadrants which have a reference angle of . And for the cos to have a negative value, the angle must terminate in the second or third quadrants. Putting these facts together we find that we want the angles that terminate the second and third quadrants which have a reference angle of  . Specifically: . Specifically:
 for the second quadrant; and for the second quadrant; and
 for the third quadrant for the third quadrant
This makes our general solution:


Notice the "3x". It came from cos(3x). 3x is the angle which terminates in the second or third quadrant with a reference anfgle of  . Notice also the " . Notice also the " ". It is the way we express the co-terminal angles. Any angle that terminates in the right quadrant with the right reference angle will work, not just ". It is the way we express the co-terminal angles. Any angle that terminates in the right quadrant with the right reference angle will work, not just  and and  . The " . The " " lets us include all the other angles without having to list them all. The "n" in " lets us include all the other angles without having to list them all. The "n" in  is a placeholder of rany integer. For each integer used for n you end up with a different angle. is a placeholder of rany integer. For each integer used for n you end up with a different angle.
The last step in the general solution is to solve for x. For this we just divide both sides by 3:


These equations are the general solution to your equation. They express all the possible solutions to your equation.
Your problem, however, does not ask for all the solutions. It only asks for solutions between 0 and  , inclusive. To find these specific solutions we take our general solution equations and try different integers for "n" until we are satisfied that we have found all the solutions between 0 and , inclusive. To find these specific solutions we take our general solution equations and try different integers for "n" until we are satisfied that we have found all the solutions between 0 and  . .
Before I start trying integers for "n", I am going to rewrite the fractions so that they all have denominators of 12. That way they will be easier to add:


Let's start with the first equation...
If we try 0 for n, we get 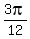 for x for x
If we try 1 for n, we get 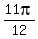 for x for x
If we try 2 for n, we get 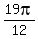 for x for x
I hope it is easy to see that if we try larger n's, that the x's will be larger than  . And if we try negative n's, that the x's will be below 0. . And if we try negative n's, that the x's will be below 0.
Now let's try the second equation...
If we try 0 for n, we get 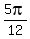 for x for x
If we try 1 for n, we get 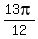 for x for x
If we try 2 for n, we get 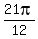 for x for x
I hope it is easy to see that if we try larger n's, that the x's will be larger than  . And if we try negative n's, that the x's will be below 0. . And if we try negative n's, that the x's will be below 0.
So the complete set of solutions to your equation that are between 0 and  are: are:
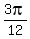 (or (or  ), ), 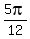 , , 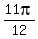 , , 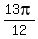 , , 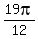 and and 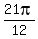 (or (or  ) )
|
|
|