|
Question 625532: Find the product for these expressions:
1. {(x+3) + y}^3
2. (a^(x+1) + b^(x-2))(a^(x+1) - b^(x-2))
In number 2, I came up with a^(x+1)^2 - b^(x-2)^2 but am little apprehensive about this. I hope you can enlighten me on both numbers.
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! 2. You are right... so far. (I hope you used the  pattern to do it easily.) You can further simplify your answer: pattern to do it easily.) You can further simplify your answer:
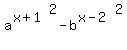
You can use the power of a power rule for exponents,  . Multiplying the exponents we get: . Multiplying the exponents we get:
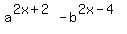
1. 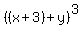
The inner set of parentheses in this expression are unnecessary. I think they are there for a reason. The slowest, hardest way to multiply this is to ignore the inner parentheses an just multiply out:
(x + 3 + y)(x + 3 + y)(x + 3 + y)
This would involve multiplying two of these trinomimals (every term of one times every term of the other and then adding like terms) and then multiplying that result by the third trinomial (again, every term times every term and then add like terms).
But I think the reason for the inner parentheses is to suggest a faster way to find the product. Parentheses say, in effect, "treat the expression inside me as a unit". In this case, it says "treat the x+3 as a unit". So when we look at 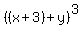 we can look at it as if it were the cube of the sum of two items: x+3 (as a unit) and y-item expression. In other "words", we can look at we can look at it as if it were the cube of the sum of two items: x+3 (as a unit) and y-item expression. In other "words", we can look at 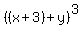 as as 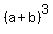 with the "a" being (x+3) and the "b" being y. with the "a" being (x+3) and the "b" being y.
Once we start looking at 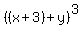 as an as an 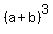 , we can start taking advantage of some of the patterns you've learned that involve powers of two-term expressions (binomials). One pattern, which is not always taught tells use how to cube a binomial: , we can start taking advantage of some of the patterns you've learned that involve powers of two-term expressions (binomials). One pattern, which is not always taught tells use how to cube a binomial:

If you know this pattern, this is the fastest, easiest way to find this product. But since you may not have learned this one, I will find the product another way first (and do it this way at the end).
A pattern you should know is  . We can use this pattern to help us find . We can use this pattern to help us find 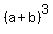 because because

and we can use the pattern on the first part. Remembering that our "a" is (x+3) and our "b" is y we can use this pattern to square ((x+3)+y):
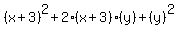
To simplify this we can use the pattern again on 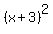 : :
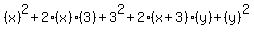
which simplifies further...
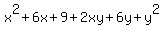
To recap our work so far:
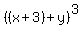
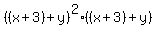
Using the pattern on the first part:

To finish we now multiply each term of the first factor times each term of the other factor and then add like terms, if any:

Simplifying:

Adding like terms and putting the terms in order from highest degree to lowest:
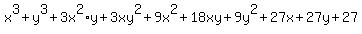
Evan faster is to us the  (if you know it): (if you know it):
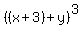
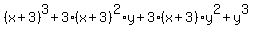
Using the pattern again on  : :

Using our  pattern on pattern on 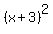 : :
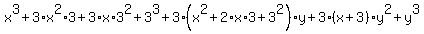
Now we simplify:
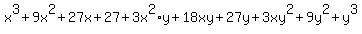
Putting terms in order from highest degree to lowest (which is not required):
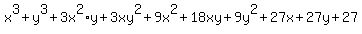
|
|
|
| |