16x² + 4y² + 96x - 8y + 84 = 0
Get the constant term off the left side by adding -84 to both sides
16x² + 96x + 4y² - 8y = -84
Swap the two middle terms
16x² + 96x + 4y² - 8y = -84
Factor out the coefficients of x² and y²
16(x² + 6x) + 4(y² - 2y) = -84
To complete the square inside the first parenhtheses,
1. Multiply the coefficient of x, which is +6 by 1/2, getting 3
2. Square this result, (3)² = +9
3. Add +9 inside the first parentheses
4. Multiply +9 by the coefficient we factored out, 16, getting +144
5. Add +144 to the right side
16(x² + 6x + 9) + 4(y² - 2y) = -84 + 144
To complete the square inside the second parenhtheses,
1. Multiply the coefficient of y, which is -2 by 1/2, getting -1
2. Square this result, (-1)² = +1
3. Add +9 inside the first parentheses
4. Multiply +1 by the coefficient we factored out, 4, getting +4
5. Add +4 to the right side
16(x² + 6x + 9) + 4(y² - 2y + 1) = -84 + 144 + 4
Factor the 1st parentheses: x² + 6x + 9 = (x + 3)(x + 3) = (x + 3)²
Factor the 2nd parentheses: y² - 2x + 1 = (y - 1)(y - 1) = (y - 1)²
Combine terms on the right: -84 + 144 + 4 = 64
16(x + 3)² + 4(y - 1)² = 64
Get a 1 on the right side by dividing through by 64
+ 
= 
+ 
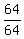
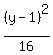= 1
+ 
= 1
To translate this equation 6 units down and 7 units to the left,
replace y by (y+6) and x by (x+7)
+ 
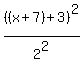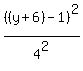= 1
+ 
= 1
+ 
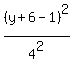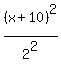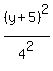= 1
Edwin
