Question 624657: The solution of 2^(2x+3) = 2^(x+1) + 3 can be expressed in the form a + log2 b where a, b equal integers.
Find the values of a and b
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! First, I can understand that this problem may be difficult to categorize. But absolute value?? What does this problem have to do with absolute value? In the future, try to choose an appropriate category for your problems. Many tutors, like me, only look for problems in the categories they prefer. So by categorizing your problem in a completely irrelevant category your problem might not even be seen by a tutor that would like to help.
Second, are your sure the problem says "where a, b equal integers" and not something like "where a, b are both integers"? I ask because the answer (as you will see shortly) does not have equal a and b values. In the future, please make sure you post your problem accurately. Some tutors may try a problem like this, not get an equal a and b, think they did something wrong and then give up. And you end up not getting any help.
Third, thank you for putting the exponents in parentheses. It makes the problem clear. Many other posters fail to do this making it impossible to know what the actual expression is.

As you have probably learned, there is often more than one way to solve a Math problem. And there may be other ways to do this one. But the only way I see is this:
Usually, when the variable is in an exponent like in this equation, logarithms are used to solve the equation. But if we start right off with logarithms:
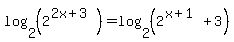
the right side becomes something I do not know how to handle. So we'll look in another direction.
The keys to this solution are:- Noticing that if the "+3" and the "+1" were gone, the 2x in one exponent would be twice as large as the x in the other exponent. An equation where one exponent is twice as large as the other is called an equation in "quadratic form". And these kinds of equations can be solved using the methods you have learned for solving quadratic equations.
- The "+3" and the "+1" can be made to disappear by a clever use of the rules for exponents.
So we will get rid of the "+3" and "+1" and then solve the resulting quadratic form equation.
To eliminate the "+3" the "+1" in the exponents we have to think: When do exponents get added? Answer: When you use the  exponent rule for multiplying. So if we think of exponent rule for multiplying. So if we think of  and the and the  as the results of a multiplication, what would have been multiplied? Answer: as the results of a multiplication, what would have been multiplied? Answer:

and

which simplify to:

and

Substituting these into our equation we get:

The equation, with exponents of 2x and x, is now in quadratic form. And we can now use methods for quadratic equations to solve it.
These methods start by making one side zero. Subtracting 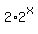 and 3 from each side we get: and 3 from each side we get:

Next we factor (or use the Quadratic Formula). Until you have done a few of these quadratic form equations it can be difficult to see how to do this. It may help to use a temporary variable, let's say "q". Let q be the be the smaller base and exponent, in this case 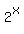 . This makes . This makes  . Substituting these in we get: . Substituting these in we get:

This is obviously a quadratic equation. And it should not be too difficult to see how to factor it:

From the Zero Product Property we get:
 or or 
Solving these we get:
 or or 
We have solved for q but we want to solve for x, Now we substitute back in for the q:
 or or 
And solve for x. Since a power of 2 cannot be negative there are no solutions to the second equation. But we can solve the first one. This is where we end up using logarithms. Finding the base 2 log of each side:

On the left side we can use the  to move the exponent in the argument out in front. (It is this property that is the reason we use logarithms on equations like this. It allows us to move the exponent, where the variable is, to a place in the expression where can then use regular algebra to solve for the variable.) On the right side we can use another property of logarithms, to move the exponent in the argument out in front. (It is this property that is the reason we use logarithms on equations like this. It allows us to move the exponent, where the variable is, to a place in the expression where can then use regular algebra to solve for the variable.) On the right side we can use another property of logarithms,  . Using both of these properties we get: . Using both of these properties we get:
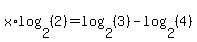
Since  and and  , ,  and and  . Substituting these in we get: . Substituting these in we get:

or just

This is the solution to your equation, with the "a" being 2 and the "b" being 3 (both integers but not equal).
After a few of these quadratic form equations you will not need a temporary variable. So you start seeing how to go directly from

to

to
 or or 
etc.
|
|
|