Question 624441: 1. How do you square a binomial?
2. Why is the product of squaring a binomial a perfect square trinomial?
3. How do you find the product of the sum and the difference of the same two terms?
4. Why do you call the product of the sum and the difference of the same two terms the difference between two squares?
I need your help on our topic about Squaring Binomials (#1-2) and the Product of the sum and the difference of the same two terms (#3-4). Please answer my question immediately. Thanks in advance!
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! A binomial is the sum of two terms, like 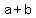 . .
You may think that sometimes there is subtraction, but it is easier to think of subtraction as just adding the opposite. I'm not kidding. Minus signs are a lot less confusing if you think of 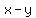 as as 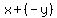 meaning meaning  plus the opposite of plus the opposite of  . .
1. The square of a binomial is calculated by multiplying the binomial times itself, but we have done it so many times that we usually skip steps, and go straight to the end result.
If I wanted to show all the steps I can think of, I would write:

So, in sum 
To square a binomial, you square each term, and then add those squares, plus twice the product of the two terms.
2. When you multiply a binomial times the same binomial to square it (as shown above), you end up with all the possible products of a term from one factor times a term from the other factor.
There are 4 products, but 2 of them 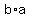 and and  are like terms (very alike, since they are the same). are like terms (very alike, since they are the same).
Because they are like terms, they can be added together (we call that "collecting like terms") to get 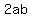 . .
Since we make 1 term out of 2 of the 4 products, we end up with 3 terms.
At that point, we cannot add terms together any more, so we have a trinomial (a sum of 3 terms). It is a perfect square because we made it by squaring an expression.
3. In algebra, we often multiply one binomial times another. Because we are so used to doing it, and we know how it is going to end, we usually skip steps and just write the final result.
Suppose we want to multiply the binomials 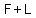 and and 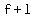 . .
They each have a first term (F or f) and a second (or last) term (L and l).
The multiplication step by step is:

The middle step is usually skipped because we figured out that the four products that we have as terms at the end are:
the product of the two  irst terms; irst terms; 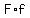 , ,
the product, 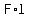 , of the two terms that were on the , of the two terms that were on the  utside of the product of binomials utside of the product of binomials 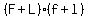 , ,
the product, 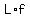 , of the two terms that were on the , of the two terms that were on the  nside of the product of binomials nside of the product of binomials 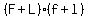 , ,
and the product 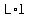 of the of the  ast terms of the binomials. ast terms of the binomials.
We are taught to use the word  to help us remember what products to include. to help us remember what products to include.
In the case were the two binomials are a sum  and a difference and a difference  of the same two expressions ( of the same two expressions ( and and  ), the two middle terms (the O and I in FOIL) are opposites. ), the two middle terms (the O and I in FOIL) are opposites.
Since they are opposites, they cancel each other. (They add up to zero).
So we end up with FL, which means Florida to me (where I'm heading to for vacation next week).
I'll show you;

We always skip the middle steps and just write

 is a difference, the result of subtracting is a difference, the result of subtracting  minus minus 
Since  and and  are squares, we say that are squares, we say that
"the product of a sum times a difference is the difference of the squares."
That can come in handy if you have to multiply certain numbers. For example,

It so happens that 35 and 25 are the sum and the difference of the same two numbers
 and and 
So 
and I can calulcate that without using pencil (or pen) and paper.
|
|
|