Question 624401: How many ways are there to choose two distinct numbers from {1,2,3,...,10} such that their product minus their sum is a multiple of 3?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! We need  to be a multiple of 3, with a and b being different integers between 1 and 10. to be a multiple of 3, with a and b being different integers between 1 and 10.
If both numbers (a and b) are multiple of 3, 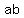 and and 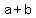 will be multiples of 3. will be multiples of 3.
As a consequence,  will be a multiple of 3. will be a multiple of 3.
That means that the 3 (un-ordered) pairs we can make with 3, 6, and 9 are solutions.
(From the wording of the problem, I am assuming that order does not matter, so choosing 3 and 6 is the same as choosing 6 and 3).
In general, we need to go into modulo 3 arithmetic, where we say that all integers are "congruent modulo 3" with the remainder from dividing them by 3.
So 3, 6, and 9 are congruent modulo 3 with 0,
1, 4, 7, and 10 are congruent modulo 3 with 1, and
2, 5, and 8 are congruent modulo 3 with 2.
We can test what happens with the congruent numbers from the set {0,1,2}.
 represents the case where a and b are both multiples of 3,and so is represents the case where a and b are both multiples of 3,and so is  . .
The other possibilities are listed below.
For the pair (1,1):  (congruent with 2 modulo 3, so it does not work. (congruent with 2 modulo 3, so it does not work.
For the pair (2,2):  which gives us more solutions. which gives us more solutions.
For the pairs (0,1) or (1,0):  (congruent with 2 modulo 3, so it does not work. (congruent with 2 modulo 3, so it does not work.
For the pairs (0,2) or (2,0):  (congruent with 1 modulo 3, so it does not work. (congruent with 1 modulo 3, so it does not work.
For the pairs (1,2) or (2,1):  (congruent with 2 modulo 3, so it does not work. (congruent with 2 modulo 3, so it does not work.
In sum, both numbers must be multiple of 3, giving us 3 ways to do it, or both numbers must be congruent with 2 modulo 3 (chosen from {2,5,8}), giving us another 3 ways to do it.
There are  ways to choose two distinct numbers from {1,2,3,...,10} such that their product minus their sum is a multiple of 3. ways to choose two distinct numbers from {1,2,3,...,10} such that their product minus their sum is a multiple of 3.
|
|
|