Question 624376: The parallel sides of a trapezoid are 8 in and 12 in long. One non-parallel side is 6 in long.
a) How far must this side be extended to meet the extension of the opposite side?
b) What are the possible lengths for the opposite side?
Thank you for your time in advance!
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! Extending the non-parallel sides until they meet forms a large triangle, containing the trapezoid, plus a smaller, similar triangle on top, looking like this:
 The 6 in long side was extended by adding x inches.
In similar triangles, the ratios of lengths for corresponding pairs of sides are the same, so
Multiplying both sides times 24, we get
 -->  --> 
a) The 6 in long side must be extended by  inches to meet the extension of the opposite side.
b) The side of the large triangle that includes the 6 in long trapezoid side is  in long.
The possible lengths (in inches) for the opposite side of the large triangle range from
 all the way to
 (not including 6 and 30).
The lengths of the non parallel sides of the trapezoid are  of the lengths of the triangle sides, so the lengths for the other side of the trapezoid could be anything between
 and  inches.
You could write it as the length, y, in inches is such that
|
|
|
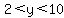
