SOLUTION: solve the following systems using cramers rule: 2x-y=7 and 3x+y=13 thanks!! :)

Algebra ->  Systems-of-equations -> SOLUTION: solve the following systems using cramers rule: 2x-y=7 and 3x+y=13 thanks!! :)      Log On


   

Question 624236: solve the following systems using cramers rule:
2x-y=7
and 3x+y=13
thanks!! :)
Answer by ewatrrr(24785) About Me  (Show Source):
You can put this solution on YOUR website!
 

Hi,




 
Solved by pluggable solver: Using Cramer's Rule to Solve Systems with 2 variables




  

  

  system%282%2Ax%2B-1%2Ay=7%2C3%2Ax%2B1%2Ay=13%29

  

  

  

  First let A=%28matrix%282%2C2%2C2%2C-1%2C3%2C1%29%29. This is the matrix formed by the coefficients of the given system of equations.

  

  

  Take note that the right hand values of the system are 7 and 13 which are highlighted here: 

  system%282%2Ax%2B-1%2Ay=highlight%287%29%2C3%2Ax%2B1%2Ay=highlight%2813%29%29

  

  

  

  These values are important as they will be used to replace the columns of the matrix A.

  

  

  

  

  Now let's calculate the the determinant of the matrix A to get abs%28A%29=%282%29%281%29-%28-1%29%283%29=5. Remember that the determinant of the 2x2 matrix A=%28matrix%282%2C2%2Ca%2Cb%2Cc%2Cd%29%29 is abs%28A%29=ad-bc. If you need help with calculating the determinant of any two by two matrices, then check out this solver.

  

  

  

  Notation note: abs%28A%29 denotes the determinant of the matrix A.

  

  

  

  ---------------------------------------------------------

  

  

  

  Now replace the first column of A (that corresponds to the variable 'x') with the values that form the right hand side of the system of equations. We will denote this new matrix 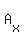A%5Bx%5D (since we're replacing the 'x' column so to speak).

  

  

  A%5Bx%5D=%28matrix%282%2C2%2Chighlight%287%29%2C-1%2Chighlight%2813%29%2C1%29%29

  

  

  

  Now compute the determinant of 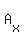A%5Bx%5D to get abs%28A%5Bx%5D%29=%287%29%281%29-%28-1%29%2813%29=20. Once again, remember that the determinant of the 2x2 matrix A=%28matrix%282%2C2%2Ca%2Cb%2Cc%2Cd%29%29 is abs%28A%29=ad-bc

  

  

  

  To find the first solution, simply divide the determinant of 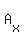A%5Bx%5D by the determinant of A to get: x=%28abs%28A%5Bx%5D%29%29%2F%28abs%28A%29%29=%2820%29%2F%285%29=4

  

  

  

  So the first solution is x=4

  

  

  

  

  ---------------------------------------------------------

  

  

  We'll follow the same basic idea to find the other solution. Let's reset by letting A=%28matrix%282%2C2%2C2%2C-1%2C3%2C1%29%29 again (this is the coefficient matrix).

  

  

  

  

  Now replace the second column of A (that corresponds to the variable 'y') with the values that form the right hand side of the system of equations. We will denote this new matrix A%5By%5D (since we're replacing the 'y' column in a way).

  

  

  A%5Bx%5D=%28matrix%282%2C2%2C2%2Chighlight%287%29%2C3%2Chighlight%2813%29%29%29

  

  

  

  Now compute the determinant of A%5By%5D to get abs%28A%5By%5D%29=%282%29%2813%29-%287%29%283%29=5.

  

  

  

  To find the second solution, divide the determinant of A%5By%5D by the determinant of A to get: y=%28abs%28A%5By%5D%29%29%2F%28abs%28A%29%29=%285%29%2F%285%29=1

  

  

  

  So the second solution is y=1

  

  

  

  

  ====================================================================================

  

  Final Answer:

  

  

  

  

  So the solutions are x=4 and y=1 giving the ordered pair (4, 1)

  

  

  

  

  Once again, Cramer's Rule is dependent on determinants. Take a look at this 2x2 Determinant Solver if you need more practice with determinants.