Hi,
The height h (in meters) of a cannonball t seconds after it is fired from a cannon is described by the equation
h(t)=-49t^2+60t.
a. What is the height of the cannonball after 4 seconds? h(4) = -544m
b. How long will the cannonball be in the air? 1.22 sec
0 = -49t^2 + 60t = t(-49t + 60)
49t= 60
t = 60/49 = 1.22 sec
Completing Square: y = ax^2 + bx + c ⇒ y = a(x -(-b/a2)^2 - a(-b/2a)^2 + c
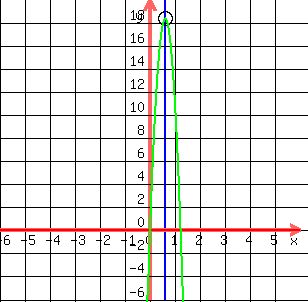
, V(60/98, 18.3673)
the vertex form of a Parabola opening up(a>0) or down(a<0), 
where(h,k) is the vertex and the Line of symmetry is x = h
c. How long does it take the cannonball to reach its maximum height? 60/98 sec
d. What is the maximum height of the cannonball? 18.3673m
