|
Question 624035: Factor a trinomial whose leading coefficient is not 1? 6x^2-17x+12
Found 2 solutions by jsmallt9, KMST:
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! As far as I know, there is no sure-fire shortcut to factoring trinomials whose leading coefficient is not a 1. But there are some ideas that can help you zero in on the right combination, if there is one. I'm not going to try to explain all possible helpful ideas but I am going to go over ones that will help with this problem.
- Let's think of this kind of factoring as "un-FOIL-ing".
- The terms in the "F" (first) positions will be factors of the squared term.
- The terms in the "L" (last) positions will be factors of the constant term (at the end).
- The middle term of the trinomial comes from adding the "O" and "I" products.
- When considering the possible factors of the constant term, remember that for every pair of factors, the negatives of each will also be factors. For example, if the the constant term is 15 not only are 3 and 5 factors but -3 and -5 are, too. Or if the constant term is -32, not only are -4 and 8 factors, 4 and -8 are, too. (Note: as long you consider positive and negative factors of the contant term, you do not have to so the same for the factors of the squared term.)
- Since the middle term is negative and since it is the sum of the "O" and "I" products, at least one of the these products must be negative.
- Since the constant term is positive its factors will either be both positive or both negative.
- Since we need a negative product and since the constant term's factors must be the same, then we must only use the pairs of negative factors of the constant term. (With this we have literally eliminated half of all the possible combinations to check!)
- The middle term has an odd coefficient. The middle term, again, is the sum of the "O" and "I" products. The only way to get an odd result when adding two numbers is to add an odd and an even number. So the "O" product must be odd and the "I" product even or vice versa.
- The only way to get an odd product is to multiply two odd numbers. Since we need an odd product we must have an "O" product or an "I" product that involves odd factors. This also reduces the possible combinations to try. For example, (6x-2)(x-6) cannot possibly work because both the "O" and "I" products have at least one even number in them so their products will both be even and, therefore, add up to an even middle term (which we do not want).
Although we still have some trial and error to do, we have reduced significantly the number of possible combinations to try. we have eliminate all pairs of positive factors of 12 and we have eliminated any combinations where both the "O" and "I" products have at least one even number. The only combinations left to try are:
(6x-1)(x-12)
(6x-3)(x-4)
(2x-1)(3x-12)
(2x-3)(3x-4)
(Note how all the "I" products will be products of two odd numbers and all the ""O" products have at least one even number in them.)
Since there were 24 possible combinations when we started, we have made a lot of progress already! And even now we can rule out one of these. Considering that any GCF's should be factored out before we even start this kind of factoring, a combination like (2x-1)(3x-12), where the 3x-12 has a common factor, cannot work. So we're down to three from 24!
With a little trial and error, we should find that 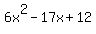 does factor into: does factor into:
(2x-3)(3x-4)
Answer by KMST(5328)   (Show Source): (Show Source):
|
|
|
| |