Question 623984: what is the general solution of cos2x=4cos^2x-sin^2x
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! Solving equations like this often involves the following steps:- Using algebra and/or Trig. properties to transform the equation into one or more equations of the following form:
TrigFunction(expression) = number
During this transformation you may or may not be able to get the equation down to a single function. If not, then make one side of the equation a zero (by adding/subtracting appropriately) and then try to factor the other side so that each factor has only one function with the same argument. (This is how you end up with multiple equations of the above form.) It can be helpful during this transformation process to use Trig. properties to reduce the number of different arguments to the functions and/or the number of different functions. - For each equation from step 1, find the general solution. Trig functions are periodic so there will usually be an infinite number of solutions to these equations. The general solution will be one or more equations that express this infinite set of solutions.
- Some problems ask for a specific set of solutions. "Find the smallest positive solution to...", "Find all solutions between
 and and  .", etc. If so, then use the general solution equations from step 2 to find the requested specific solutions. .", etc. If so, then use the general solution equations from step 2 to find the requested specific solutions.
Let's see this in action:
1. Transformation.
In your equation

we start with two functions, cos and sin, and two arguments, 2x and x. Looking ahead I can see that if we make one side zero, not will we not be able to factor the other side. So we'll start by reducing the number of different arguments. (It's usually better start start with this before your try to reduce the different functions.) We can use the cos(2x) formula to change that argument into argument(s) of just x. There are three variations of this formula:Any one of them will work. Looking ahead I can see that the first one will make things easier later on. It will quickly allow me to reduce the number of functions, too. So we'll replace cos(2x) with the first variation:

As you maybe see now, we can get rid of the sin's by adding  to each side: to each side:

So we have quickly reduced the equaiton down to a single function, cos, with a single argument, x. We can use some simple algebra to finish the transformation into the desired form. Subtracting  form each side: form each side:

Divide both sides by 3:

Square root of each side. (Since zero only has zero as a square root, we don't have to be concerned with the negative square root.)
0 = cos(x)
We have finished the transformation.
2. Find the general solution for each equation from step 1.
We only have one equation, cos(x) = 0, so this will not be as hard as some problems. And a zero value for cos should be recognized as a special angle value for cos. So we will not need our calculator. The general solution equations for
TrigFunction(expression) = number
will take on the following form:
expression = A + 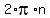
where "expression" is the argument to the function in TrigFunction(expression) and "A" is an angle whose function value is the number from TrigFunction(expression) = number. There will be an equation of this form fo revery angle with the right function value and with a different terminal side. (Most of the time this will mean two general solutions equations for each "TrigFunction(expression) = number" equation. Note: If "expression" is not just "x" then take these equations and use algebra to solve for "x".
We should know that  and and  have different terminal sides but they both have a cos value of 0. So our general solution equations for cos(x) = 0 are: have different terminal sides but they both have a cos value of 0. So our general solution equations for cos(x) = 0 are:

and

Notes on the general solution:- We did not have to use
 . We could have used any angle that terminates at the same place as . We could have used any angle that terminates at the same place as  . For example, . For example, 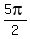 or or 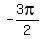 , etc. , etc. - We did not have to use
 . We could have used any angle that terminates at the same place as . We could have used any angle that terminates at the same place as  . For example, . For example,  or or  , etc. , etc. - The "n" in these equations is how we are able to express the infinite number of solutions without having to list them all. The "n" can be replaced by any integer. Each different integer will result in a different x (that is still a solution to the equation!). By going through, in theory, all the infinite number of integers, we end up with the infinite number of angles that terminate at the right place.
- Some books/teachers use a letter different from "n", like "k". Which letter you use is not important. Whatever letter is used, it is still a placeholder for integers.
- The "+
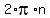 " is a way to express co-terminal angles. So " is a way to express co-terminal angles. So
 says "x is pi/2 or any angle co-terminal with says "x is pi/2 or any angle co-terminal with 
3.Specific solution.
Your problem asks only for the general solution so this step is not needed. If there had been a requested specific solution, then we would take each equation from the general solution and try various integers for "n" until we were satisfied that we had found all the requested specific solutions.
P.S. In case we used a different variation of the cos(2x) formula...


If we get one side to be zero (by subtracting 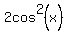 and adding 1): and adding 1):

we still will not be able to factor this. So we should reduce the number of functions. Fortunately it is easy to turn  into into  (and vice versa): (and vice versa):

Note the use of parentheses when making the substitution. This is extremely important when substituting a multiple-term expression like 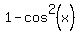 for single-term expression like for single-term expression like  . In this case we can see that we need to subtract the 1 and the . In this case we can see that we need to subtract the 1 and the 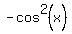 . Subtracting correctly we get: . Subtracting correctly we get:

which is the same as we got earlier (only after a little extra work).
|
|
|