|
Question 623930: I need help in finding what H, K , R. Also finding the center of the circle.
Find the center (h, k) and the radius r of the circle
4 x^2 - 7 x+ 4 y^2 - 8 = 0 .
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! The standard form for the equation of a circle is:

So to find the h, k and r for your circle we must transform

into the standard pattern. To get the 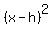 and and 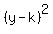 we must do what is called "complete the square". Although this can be done in different ways, the most common one is this: we must do what is called "complete the square". Although this can be done in different ways, the most common one is this:- Gather the variable terms on one side of the equation. In other words, move any non-variable (i.e. constant) terms to the other side.
- If possible, turn the coefficients of the squared terms into 1's. (For circles, this will be possible. For other conic sections (ellipses, hyperbolas and parabols it will not be possible.)
- For each variable find 1/2 of the coefficient of the first power term. IOW, find 1/2 of the "x" term or the "y" term. Remember what this 1/2 number is because you will be using it later.
- Square the 1/2 number from the previous step.
- Add the squares from the previous step to each side of the equation. (This step can actually be very tricky if we were not able to turn the coefficients of the
 and and  terms into 1's earlier. Fortunately, with a circle, this step is easy.) terms into 1's earlier. Fortunately, with a circle, this step is easy.) - Rewrite the x terms and the y terms into binomial squares:
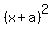 and and 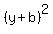 using the remembered "1/2 numbers" from step 3 for the "a" and "b". using the remembered "1/2 numbers" from step 3 for the "a" and "b".
Let's see this in action:
1. Move the constant term.
Adding 8 to each side we get:

2. Turn the coefficents of the squared terms into 1's.
Dividing both sides by 4 we get:

3. Find the "1/2 numbers".
1/2 of -7/4 (do you see why the coefficient of x is negative 7/4?) is -7/8. There is no y term (just a  term). So we can consider the y term to be 0y. 1/2 of zero is zero. term). So we can consider the y term to be 0y. 1/2 of zero is zero.
4. Square the "1/2 numbers"
 and zero squared is still zero. and zero squared is still zero.
5. Add the squared numbers to each side.
Adding 49/64 and 0 to each side:

Note how I placed the squared numbers on the left side. I put them next to the teems we used to find the squared numbers.
6. Rewrite as binomial squares.
Using our "1/2 numbers" from step 3 we get:

We have now completed the squares. We have two more things to do:- Rewrite the binomial squares as subtractions (because the standard form has them as subtractions); and
- Simplify the right side and rewrite it as a perfect square.
1. Rewrite as subtractions:

Make sure you see how these are the same as the addtions we had earlier.
2. Simplify and rewrite the right side:



Simplifying the square root...


We have finally reached the standard form for the equation of a circle. From this we can just read the h, k and r:



So the center is (7/4, 0) and the radius is 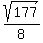 . .
|
|
|
| |