SOLUTION: please help solve this problem, thank you Factor completely. If a polynomial is prime, state this 9t^2+14t+5

Algebra ->  Polynomials-and-rational-expressions -> SOLUTION: please help solve this problem, thank you Factor completely. If a polynomial is prime, state this 9t^2+14t+5      Log On


   

Question 623136: please help solve this problem, thank you
Factor completely. If a polynomial is prime, state this
9t^2+14t+5
Answer by jsmallt9(3758) About Me  (Show Source):
You can put this solution on YOUR website!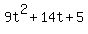
9t%5E2%2B14t%2B5
The greatest common factor here is 1. And we rarely bother factoring out a 1.

Now we move on to other factoring techniques. One of these techniques is to use a factoring patterm:
  • Difference of squares: a%5E2-b%5E2+=+%28a%2Bb%29%28a-b%29
  • Sum of cubes: a%5E3%2Bb%5E3+=+%28a%2Bb%29%28a%5E2-ab%2Bb%5E2%29
  • Difference of cubes: a%5E3-b%5E3+=+%28a-b%29%28a%5E2%2Bab%2Bb%5E2%29
  • Perfect square trinomials:
    • a%5E2%2B2ab%2Bb%5E2=+%28a%2Bb%29%5E2 [or (a+b)(a+b)]
    • a%5E2-2ab%2Bb%5E2=+%28a-b%29%5E2 [or (a-b)(a-b)]
The first three patterns have two terms on the un-factored side. Your expression has three terms so we cannot use them.

The last two patterns have three terms so they may work. Your expression has a pattern of "+" then "+" then "+". This matches the pattern of pluses and minuses in the a%5E2%2B2ab%2Bb%5E2 pattern.

Next we check to see if each individual term of your expression also matches each term of the a%5E2%2B2ab%2Bb%5E2 pattern.

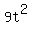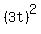The first term of of the pattern is a%5E2. Is your first term, 9t%5E2, a perfect square? Answer: Yes. It is %283t%29%5E2. This makes your "a" a "3t".

The third term of of the pattern is b%5E2. Is your third term, 5, a perfect square? Answer: No. So your expression does not match any of the patterns. So we move on to another factoring method.

Another factoring method you learn is factoring trinomials of the form ax%5E2%2Bbx%2Bc. Your expression has this form so this method may work.

This method could be called "reverse FOIL" (a name I made up) because that is the idea behind it. We are trying to see if 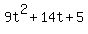9t%5E2%2B14t%2B5 is the result of FOIL-ing factors of the form:
(___ + ___)(___ + ___)

If this method factors with 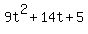9t%5E2%2B14t%2B5, then:
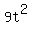  • The first term, 9t%5E2, is the result of the "F" of FOIL. (IOW, it is the result of multiplying the first terms. The factors of 9t^2 are either 3t and 3t or t and 9t. So one of these pairs will be the first terms in:
    (___ + ___)(___ + ___)

  • The last term, 5, is the result of the "L" in FOIL (i.e multiplying the last terms. The factors of 5 are 1 and 5 or -1 and -5. (Always consider the negative factors on the "L" terms. So one of these pairs will be the last terms in
    (___ + ___)(___ + ___)

  • And the middle term is the result of adding the "O" and "I" parts of FOIL. This is the key. We have several pairs of numbers to try for the first and last terms of:
    (___ + ___)(___ + ___)

    But only one (or none) of them will result in the right middle term.
These days this method is often taught using a box. The box is just a way to help you to try to find the right combination of first and last terms. I'm not going to try to draw boxes. With a little trial and error we will find that there is a combination that works:
(9t+5)(t+1)
because:
"O": 9t*1 = 9t
"I": 5*t = 5t
"O" + "I" = 9t + 5t = 14t Check!

So
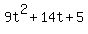
9t%5E2%2B14t%2B5
factors into
(9t+5)(t+1)

Note: If we were unable to find a combination that worked, then we would have to move on to other methods of factoring. If you run out of methods, then the expression will not factor (i.e. it is prime).