Question 623118: . A student is taking a 5 question True-False quiz but he has not been doing any work in the course and does not know the material so he randomly guesses at all the answers.
a) What is the probability that he gets the first question right?
b) What is the probability that he gets the first three questions right?
c) What is the probability that he gets at least one question right?
First of all, I don't understand the difference between Question a and Question c. Also, I read some other examples but I do not get yet on this website and my book, and still can not answer these questions.
So far I have done this
P= .5 since they are true and false.
n= 10 since they are 10 question
But I dont know how to use this data. help please!!
Found 2 solutions by Theo, jsmallt9:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! 5 question test.
true or false answer on each question.
student randomly guesses each answer.
probability of getting the question right is 50%
probability of getting the question wrong is 50%
a) What is the probability that he gets the first question right?
probability he gets the first question right is 1/2.
b) What is the probability that he gets the first three questions right?
probability he gets the first 3 questions right is 1/2 * 1/2 * 1/2 = 1/8
c) What is the probability that he gets at least one question right?
probability he gets at least one question right is equal to 1 minus the probability he gets no questions right.
probability he gets no questions right is 1/2 * 1/2 * 1/2 * 1/2 * 1/2 * 1/2 which is equal to 1/2^5 whgich is equal to 1/32.
probability he gets at least 1 question right is 1 minus 1/32 which is equal to 31/32.
since this is a 5 question test, n would be equal to 5, not 10.
that last question deals with the binomial distribution probabilities.
here's how it works.
p is equal to the probability of getting it right which is equal to .5
q is equal to the probability of getting it wrong which is equal to 1 - .5 which is equal to .5
just so happens those probabilities are the same but don't have to be.
n is equal to 5.
C(n,x) is the combination formula which is equal to n! / (x! * (n-x)!)
binomial distribution for this problem would be:
p(0 right) = C(5,0) * .5^0 * .5^5 = 1 * 1 * .03125 = .03125
P(1 right) = C(5,1) * .5^1 * .5^4 = 5 * .5 * .0625 = .15625
p(2 right) = C(5,2) * .5^2 * .5^3 = 10 * .25 * .125 = .3125
p(3 right) = C(5,3) * .5^3 * .5^2 = 10 * .125 * .25 = .3125
p(4 right) = C(5,4) * .5^4 * .5^1 = 5 * .0625 * .5 = .15625
p(5 right) = C(5,5) * .5^5 * .5^0 = 1 * .03125 * 1 = .03125
add up all the probabilities and they should be equal to 1.
they are.
probability of getting at least 1 right is equal to 1 minus .03125 which is equal to .96875 which is equal to 31/32.
probability of getting at least 1 right is equal to p(1) + p(2) + p(3) + p(4) + p(5) which is equal to the same things.
part a is only asking you for the probability of getting the first one right and doesn't consider whether the others are right or wrong so you deal with that separately.
part b is only asking you for the probability of getting the first 3 right and doesn' consider whether the others are right or wrong so you deal with that separately.
the last questions deals with the binomial distribution and you use the formula for that.
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! a) As you already figured out, the probability of randomly guessing a true/false question is 0.5 or 1/2
b) The probability of getting all of the first three questions right is the product of the probabilities of getting each one right:
0.5*0.5*0.5 = 0.125 or 1/8
c) Are there 5 questions or 10? At the beginning you say there are 5 but then later you say there are 10. Since I do not know which, I will just tell you how to find the answer.
These problems where you are to "find the probability of at least 1 ..." can be done by finding the probability of exactly 1 right, the probability of exactly 2 right, etc. and then adding all of them together to find the probability of at least one. It can be done this way but those probabilities are not easy to figure out and you would n of those probabilities to calculate.
Fortunately there is a much easier way. It takes advantage of the fact that all the probabilities of all the possible events always add up to 1. The only event, other than getting at least one right, is that he gets none right. (Think about it.) So:
P(at least one right) + P(none right) = 1
or
P(at least one right) = 1 - P(none right)
It is much easier to find just the one probability and then subtract it from 1.
So we will find the probability of getting none right. On a true/false test the probability of getting a question wrong is the same as the probability of getting it right: 0.5. The probability of getting all n questions wrong would be the product of n 0.5's, or 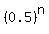 . This makes the probability of getting at least one right: . This makes the probability of getting at least one right:
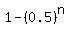
Now just use your calculator and the correct value for n to figure out the answer.
|
|
|