SOLUTION: How do I simplify ^3sqrt72*t^8 by factoring? I get confused with these problems, any help will be greatly appreciated.

Algebra ->  Square-cubic-other-roots -> SOLUTION: How do I simplify ^3sqrt72*t^8 by factoring? I get confused with these problems, any help will be greatly appreciated.      Log On


   

Question 622829: How do I simplify ^3sqrt72*t^8 by factoring? I get confused with these problems, any help will be greatly appreciated.
Answer by jsmallt9(3758) About Me  (Show Source):
You can put this solution on YOUR website!
"^3sqrt"???
I'm guessing you mean cube root: 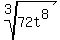root%283%2C+72t%5E8%29. If so, then the 3 is not an exponent. It is called the index of the radical and it tells you which kind of root it is. sqrt is fine for square roots. For other kinds of roots...
  • Use come English in addition to the Math syntax. For example
    "cube root of (72t^8)"
  • Teach yourself the syntax used by algebra.com's formula drawing software. Click on the "Show Source" link above to see what I typed for the following:
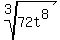
    root%283%2C+72t%5E8%29
    sqrt%283x%5E6%29 (A "missing" index is assumed to be a 2 (for square root))
    root%285%2C+32x%5E4%29

To simplify any kind of root, you look for factors (other than 1) of the radicand that are powers of the type of root. ("Radicand" is the name for the expression inside a radical. Your radicand is 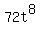72t%5E8.) So for your cube root we will look for factors of the radicand that are perfect cubes. Look for factors of the coefficient and the variables separately:
There are many factors of 72: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36 and 72. But among these there are only 2 perfect cubes: 1 and 8 (because 1+=+1%5E3 and 8+=+2%5E3. And since factoring out 1 does nothing we do not use it to simplify radicals. So the only perfect cube factor of 72 that we use is 8. So we will factor the 72 into 8*9.

Factoring variables into perfect cubes is fairly easy. If the exponent on the variable is less than 3 then there are no perfect cube factors. For exponents greater than 3 we just break up the expression into perfect cubes and a "remainder". as follows:
t%5E8+=+t%5E3%2At%5E3%2At%5E2

Putting this all together:
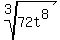
root%283%2C+72t%5E8%29
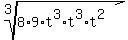
root%283%2C+8%2A9%2At%5E3%2At%5E3%2At%5E2%29
While it is not required, I like to use the Commutative Property to change the order so that all the perfect cube factors are in front:
root%283%2C+8%2At%5E3%2At%5E3%2A9%2At%5E2%29

Next we we a property of radicals, root%28a%2C+p%2Aq%29+=+root%28a%2C+p%29%2Aroot%28a%2C+q%29 to split up the radical. We want each perfect cube factor to be in its own cube root. The factors that are not perfect cubes can be all lumped into one radical.
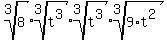
root%283%2C+8%29%2Aroot%283%2C+t%5E3%29%2Aroot%283%2C+t%5E3%29%2Aroot%283%2C+9%2At%5E2%29

Now we replace the cube roots of the perfect cubes:
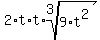
2%2At%2At%2Aroot%283%2C+9%2At%5E2%29
which simplifies to:
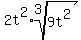
2t%5E2%2Aroot%283%2C+9t%5E2%29