Question 622692: Find the value of the expression: 125^(log5)^3
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! What you posted says/means:
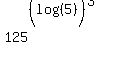
What I think you meant is:

If I am wrong, then I apologize. You'll have to re-post your question.
If I am right, then- The solution is below.
- The "3" in
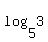 is not an exponent, even though it may look like one. Logarithms can be difficult to post on algebra,com. Your best options are: is not an exponent, even though it may look like one. Logarithms can be difficult to post on algebra,com. Your best options are:- Use some English to supplement the Math syntax. For example:
"(base 5 log of 3)" would be a good way to describe 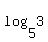 - Teach yourself the syntax used by algebra.com's formula drawing software. Click on the "Show source" link above to see what I type for these logs:
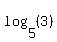
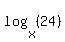
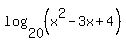
To understand this solution let's try to understand what logarithms are a little better. Logarithms are exponents. The idea behind logarithms is that it is possible to take any positive number (except 1) and, if you raise it to the right power, you can get any other positive number as a result. The syntax:

read literally means "base a logarithm of q". But it is more useful to to think of

as: the exponent you would put on "a" to get a result of "q". For example: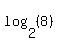 is the exponent you would put on a 2 to get an 8. We know this exponent. is the exponent you would put on a 2 to get an 8. We know this exponent.  . So . So  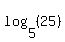 is the exponent you would put on a 5 to get a 25. We know this exponent. is the exponent you would put on a 5 to get a 25. We know this exponent.  . So . So  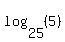 is the exponent you would put on a 25 to get a 5. We know this exponent (if we remember what exponent a square root is). is the exponent you would put on a 25 to get a 5. We know this exponent (if we remember what exponent a square root is).  . So . So  ) ) is the exponent you would put on a 5 to get a 6. We do not what this exponent is. But the idea of logarithms is that there is such an exponent. is the exponent you would put on a 5 to get a 6. We do not what this exponent is. But the idea of logarithms is that there is such an exponent.
In some ways logarithms are like square roots:- We know that they exist.
- Some of them we know:
 , ,  , ,  , ,  (because (because  ), etc. ), etc. - Some of them we do not know exactly (even though they do exist):
 , ,  , , 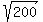 , , 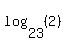 , etc. , etc.
Since we do not know these we cannot replace them with simple number. For these we are "stuck" with the awkward syntax of logarithms and square roots. (If we need a decimal approximation for these we can use our calculators.)
Once we have a better idea about what a logarithm represents it gets much easier to work with them. In particular it will be easier to understand (and remember):
 for all possible a's and q's. for all possible a's and q's.
The left side says: "a" raised to the power that you would put on "a" to get a result of "q". Once we get this, it is easy to understand why the result is equal to "q". We will use this property of logarithms to solve you problem.
In order to use the  pattern we must match the base of the exponent with the base of the logarithm (the a's). To use this on pattern we must match the base of the exponent with the base of the logarithm (the a's). To use this on

we will need to do one of the following:- Change the 125 to a 5
- Change the 5 to 125
- Change both the 125 and the 5 to some third number.
Once we realize that  it will be easy to see how to change the 125 into a 5 (or vice versa). Replacing the 125 with it will be easy to see how to change the 125 into a 5 (or vice versa). Replacing the 125 with 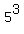 we get: we get:

The rule for exponents when raising a power to a power is to multiply the exponents. So this becomes:

We now have the bases matched. But the pattern,  , does not have a number in front of the logarithm. So we need to find a way to get rid of the exponent in front of the log. Fortunately, another property of logarithms, , does not have a number in front of the logarithm. So we need to find a way to get rid of the exponent in front of the log. Fortunately, another property of logarithms,  , allows us to move a number in front into the argument as its exponent: , allows us to move a number in front into the argument as its exponent:
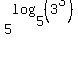
And since  this becomes: this becomes:

We have now matched the pattern of  . So . So
 must be 27. must be 27.
|
|
|