Question 62263: I am lost on this one
Solve 3x^2-x-4<_0
thank you for your time
Found 2 solutions by stanbon, funmath:
Answer by stanbon(75887)   (Show Source):
You can put this solution on YOUR website! 3x^2-x-4<=0
(3x-4)(x+1)<=0
The equality is satisfied if x=3/4 or x=-1
Draw a number line and plot the values x=-1 and x=3/4
That creates three intervals on the number line:
I: (-inf,-1)
II: (-1,3/4)
III; (3/4,inf)
Test a point in each interval to see where
the solution set for the inequality lies.
I: test x=-10 in 3x^2-x-4<0; it does not work
II: test x=0 in the same; it works
III: test x=10 in the same; it does not work
SOLUTION:
-1<=x<=3/4
Cheers,
Stan H.
Answer by funmath(2933) (Show Source):
You can put this solution on YOUR website! Solve  Factor first.
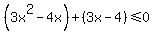
 Find the critical numbers that make this equal 0.
x+1=0 and 3x-4=0
x+1-1=0-1 and 3x-4+4=0+4
x+0=-1 and 3x-0=4
x=-1 and 3x=4
x=-1 and 3x/3=4/3
x=-1 and x=4/3 The critical numbers tell you the intervals to test.
(-infinity,-1], [-1,4/3],[4/3,infinity)
Choose a test point in the interval, if the statement is true, then that interval is part of the solution, if not, it's not.
For (-infinity,-1] test -2.
 This is false, so this interval is not part of the solution.
:
For [-1,4/3] test 0.
 This is true, so the interval [-1,4/3] is part of the solution.
:
For [4/3,infinity) test 2
 This is false, so this interval is not part of the solution.
:
Therefore, the solution set is: [-1,4/3].
:
Note that if the inquality symbol was reversed the solution set would be the two intervals that we rejected. It is possible to have more than one interval as your solution set.
Happy Calculating!!!
|
|
|
