Question 622504: please help me solve:
4tan^2u-1= tan^2u
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
Let me change the name of  for a little while, to save ink and confusion. for a little while, to save ink and confusion.

Now I can write the confusing equation as
 --> -->  --> -->  --> --> 
Back into trigonometry,

You should know an angle that is a solution.
(You should sine and cosine of 0, 30,45,60, and 90 degrees, or at least have a chart with their exact values handy).
 or or  is a solution. is a solution.
 , ,  , and , and 
(although teachers prefer the equivalent expression  because they do not like square roots in denominators). because they do not like square roots in denominators).
You also should know that the supplementary angle,  or or 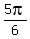 has the opposite tangent: has the opposite tangent:

So those two angles are solutions.
There are many more solutions, because the tangent function has a period of  or or  , so to include all solutions we need to add , so to include all solutions we need to add 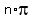 with with  defined as an integer to the solutions above. defined as an integer to the solutions above.
(I am not going to continue with the degrees, because I'm sure your teacher likes pies better than degrees).
In radians, and putting all solutions in one formula, my solution set is
 for all n integers for all n integers
|
|
|