Question 622148: solve the inequality 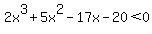
Found 2 solutions by matineesuxxx, lwsshak3:
Answer by matineesuxxx(27)   (Show Source): (Show Source):
You can put this solution on YOUR website! in order to solve this type of inequality, the easiest way is the turn it into an EQUALITY and factor, assuming you know the factor theorem, i can see right off the bat that x = -1 sets the equation equal to zero. so now that you know (x+1) is a factor, solve the rest with either long division or synthetic division. im also going to assume you know how to use long division and or synthetic division to factor this function.
after all that you will get the factored form 0 = (x+1)(2x-5)(x+4) , so now you know that the zeros are X= -1, 5/2, and -4 , you can also see that they are all first order, which is nice. now since the leading coefficient is positive ( 2 > 0) and this is a cubic, we know that is starts in the 3rd quadrant and leaves in the first. so this function is less than zero for every x less than -4 ( X<-4) and when x is between -1 and 5/2. so, 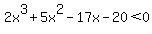 when ( -4 > X) and ( -1 < X < 5/2) when ( -4 > X) and ( -1 < X < 5/2)
Answer by lwsshak3(11628)   (Show Source): (Show Source):
You can put this solution on YOUR website!
solve the inequality
2x^3+5x^2-17x-20<0
To solve this problem, the equation must be in factored form.
This seems like a difficult expression to factor and probably it could be done with the rational roots theorem, but I'm just going to use a graphing calculator to find the following factors of this problem:
2x^3+5x^2-17x-20<0
(x+4)(x+1)(2x-5)<0
number line:
<..-...-4....+.....-1....-....5/2.....+.......>
solution:
(-∞,-4) U (-1,5/2)
|
|
|