SOLUTION: I need to learn this with the reinforcement of detailed instructions on how to get to these final results. Thank you. The monthly value of a share of ACME Corporation, in dollar

Algebra ->  Quadratic Equations and Parabolas -> SOLUTION: I need to learn this with the reinforcement of detailed instructions on how to get to these final results. Thank you. The monthly value of a share of ACME Corporation, in dollar      Log On


   

Question 622091: I need to learn this with the reinforcement of detailed instructions on how to get to these final results. Thank you.
The monthly value of a share of ACME Corporation, in dollars, since January 2009 are shown in the table below. The values of the table below model the behavior of a quadratic function when it is graphed.
Month ------ Share Value (in dollars)
0 ------ 55
3 ------ 16
5 ------ 0
7 ------ -8
9 ------ -8
11 ------ 0
13 ------ 16
15 ------ 40
1. Using the table above, find the quadratic equation that represents the monthly value of a share of ACME Corporation since January 2009. Use the variable x to represent the number of months after January 2009 and the variable y to represent the monthly value
2. Find the y-intercept. Interpret the meaning of the y-intercept in relation to the given real-life scenario
3. Find the x-intercepts. Interpret the meaning of the x-intercepts in relation to the given real-life scenario.
4. From the equation you found in problem 1, what is the concavity of the parabola? How do you know? What is the lowest or maximum monthly value of a share of ACME Corporation and when did that occur?
5. Using the quadratic equation you found in problem 1, predict the value of a share of ACME Corporation in October 2010?
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
If this was a real life set of data, I would first plot the points to see what shape they suggest. Next, I would use some computer software to do linear regression and find the fit of the functions that I suspect best fit the data points.
If I only had pencil and paper. I would hand-draw a smooth curve that fit the points, and use my knowledge of math to figure out an equation for the function that represents the data.
The problem says it's a quadratic function, so we need to do none of that.

1. Three points determine a quadratic function (we may have to solve a system of equations to find coefficients), and all points would be used to verify the fit.
A quadratic function can be represented as
y=ax%5E2%2Bbx%2Bc or
y=a%28x-k%292%2Bh with x=k being the axis of symmetry and (k,h) being the coordinates of the vertex.
If y=0 for x=s and x=t, then quadratic polynomial can be factored, and the function could be represented as
y=a%28x-s%29%28x-t%29.
We have that last option, and it may be the easiest way to solve the problem.
We have y=a%28x-11%29%28x-5%29 and we just have to find a.
For x=0,
y=a%28-11%29%28-5%29=55a=55 --> a=1
So y=%28x-11%29%28x-5%29 or y=x%5E2-16x%2B55 could be the answer.
We may want to express it in another way,
completing the square for 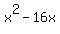x%5E2-16x like this
y-55=x%5E2-16x --> y-55%2B64=x%5E2-16x%2B64 --> y%2B9=%28x-8%29%5E2 --> highlight%28y=%28x-8%29%5E2-9%29
The second option works well too, because the data suggests that the axis of symmetry is x=8, so we expect the equation to be
y=a%28x-8%29%5E2%2Bh.
With the (x,y) coordinates of a couple of points we could set up a system of equations and find a and h.
For x=9, y=a%289-8%29%5E2%2Bh=a%2Bh=-8 and
For x=11, y=a%2811-8%29%5E2%2Bh=a%2A3%5E2%2Bh=9a%2Bh=0
give us system%28a%2Bh=-8%2C9a%2Bh=0%29 which gives us a=8 and h=-9,
so we get highlight%28y=%28x-8%29%5E2-9%29
2. The y-intercept is the y value when x=0. It is y=55. It is the share value for x=0, month zero, January 2009.
3. The x-intercepts are the x values where y=0, x=7 and x=9. The share value was zero at months 7 and 9 after January 2009. That happened on August and October 2009.
4. The equation has a negative coefficient a, so the parabola opens up. It's concave upwards, and the graph looks like a smile. The lowest point is the vertex (8,-9). It represents the lowest share value (-0), which occurred at month 8, in September 2009. The value of a share of ACME Corporation was -$9 then.