SOLUTION: I don't get how I should start solving this... If the random variable z is the standard normal score and P(z > a) > 0.5, then a > 0. Why or why not?

 

Hi,

If the random variable z is the standard normal score and P(z > a) > 0.5, then a > 0.

Note: when z > 0, then P(z) > .50 (Area under the standard normal curve to the 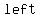 of the z- value >50%

 P(z > a) > .50, then a < 0, so as the Area to the right would be > .50



Here is the standard normal curve. z=values of 0,±1, ±2,±3 shown

for ex: 50% of the area under the normal curve is to the left and right of z=0

one  standard deviation from the mean(z= ±1)  accounts for about 68.2% of the set 

two standard deviations from the mean(z= ±2) account for about 95.4%

and three standard deviations from the mean(z= ±2) account for about 99.7%.