SOLUTION: Please help.. X has a normal distribution with a mean of 80.0 and a standard deviation of 3.5. Find the following probabilities: (A) P(x < 75.0) (B) P(75.0 < x < 84.0) (C

 

Hi,

X has a normal distribution with a mean of 80.0 and a standard deviation of 3.5. 

z = 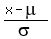  Here am using Excel NORMSDIST function to determine z=values 

(which determines % of the area under the standard normal curve to the left of that z-value)

(A) P(x < 75.0) = P(z< -5/3.5)) = P(z<-1.4286) = .0766  or 7.66%

(B) P(75.0 < x < 84.0) = P(-1.4286 < z < 4/3.5) = .8735 - .0766

(C) P(x > 87.0) = 1 -P(z < 7/3.5) = 1 - NORMSDIST(2) =  .0228  or 2.28%

Here is the standard normal curve. z=values of 0,±1, ±2,±3 shown

for ex: 50% of the area under the normal curve is to the left and right of z=0

one  standard deviation from the mean(z= ±1)  accounts for about 68.2% of the set 

two standard deviations from the mean(z= ±2) account for about 95.4%

and three standard deviations from the mean(z= ±2) account for about 99.7%.