Question 621365: can you give me an example of coin problew with solution and answer?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! There are different kinds of coin problems. The most popular type involves just solving equations. A simple problem of that kind, designed to involve a system of linear equation would be
A coin jar containing 17 coins, including only quarters and nickels (25 cent and 5 cent coins for those not familiar with US currency) is found to contain $2.25. How many coins of each kind were in the jar?
DEFINE VARIABLES
You start by defining variables for the numbers you need to find.
Let  be the number of nickels and be the number of nickels and  be the number of quarters. be the number of quarters.
SET UP EQUATIONS
Then you set up an equation for the total number of coins:

and another for the total amount of money.
I would express amounts of money in cents to be able to have just integers in the equation, which would be
 . .
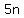 represents the amount of cents in represents the amount of cents in  nickels and nickels and
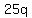 represents the amount of cents in represents the amount of cents in  quarters. quarters.
That last equation could be simplified by dividing by 5 both sides of the equal sign:
 --> -->  . .
The two equations form the system of linear equations
 . .
SOLVE THE SYSTEM OF EQUATIONS
In the system above you have 2 variables and 2 equations, and you expect to find one answer set involving integer solutions. (To have solutions that make sense in relation to the word problem, teachers set problems up so that it will be so).
The system can be easily solved by substitution or by elimination.
BY SUBSTITUTION:
You solve one equation for one of the variables (let's try for  ) )
 --> --> 
and substitute the expression found for that variable in the other equation
 --> -->  --> --> 
Now you have an equation involving only the other variable ( ) . ) .
Then you solve for the other variable ( ) )
 --> -->  --> -->  --> -->  --> --> 
Next, you substitute the value found in one of the earlier equations.
(I'll use  because it lead to the solution faster). because it lead to the solution faster).
 --> -->  --> -->  . .
BY ELIMINATION:
You combine the equations by multiplying them by factor as needed and the adding them (adding left side to left side and right side to right side).
 --(top equation times (-1))--> --(top equation times (-1))-->  --> -->  --> ... --> --> ... --> 
The work in the ... is the same as for the substitution method, and the work beyond that could be similar, leading to  . .
The theory says that you can replace one of the equation in a system with a combination of equations without gaining solutions, so we would from
 to to  . .
Then we could crossover to substitution (and proceed as above), or persist with elimination, combining equations, multiplying
 by (-1) and adding it to by (-1) and adding it to  to get to get  . .
|
|
|