Question 620914: Using complete sentences, explain how to factor each one. Be sure that the final factorization (or "answer") is a part of your explanation.
10x2 − 7x − 3
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! This is how I do it.
To factor the quadratic trinomial 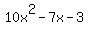 , ,
I first multiply together the absolute values of the leading coefficient (10) and the independent term (-3) to get  . .
I look for, and list all pairs of factors that multiply to yield that product, and find 4 such pairs:



 . .
One of those pairs will be the absolute values of the coefficients of first degree terms obtained when multiplying the final factorization.
Because the independent term (-3) is negative, I know that those coefficients of first degree terms have opposite signs.
I also know that they add up to the coefficient of the first degree term in the original polynomial (-7).
From the four pairs of factors found above, the pair of factors, with signs, that add up to -7 is
 . .
The expanded product of the factorization will contain 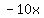 and and 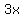 in addition to the leading and independent terms in addition to the leading and independent terms  and and  . .
I then organize the expanded product of the factorization in a 2 by 2 square, with the newly found terms at opposite corners:

Next, I look for common factors for each row and column and write them on the same row/column, outside the square.
I find  as a common factor for as a common factor for  and and 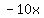 , so I write , so I write  to the left of to the left of  . .
I find  as a common factor for as a common factor for  and and  , so I write , so I write  to the left of to the left of  . .
I write  above above  and and 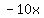 , because it is their common factor. , because it is their common factor.
I write  above above 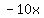 and and  , because it is their common factor. , because it is their common factor.

Now I make a binomial of the terms written above the square  and another binomial with the terms written to the left of the square and another binomial with the terms written to the left of the square 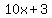 . .
I multiply those binomials to verify that the terms inside the square are generated.
I also verify that collecting terms in that product produces the original trinomial.

|
|
|