Hi,
Show that one and only one out of n, n+2, n+4 is divisible by 3, where n is any positive integer
Note: number  must leave a remainder of either 0, 2, or 4 when divided by 3,
must leave a remainder of either 0, 2, or 4 when divided by 3,
so it can be written as either 3k, 3k+2, or 3k+4 for some k (the quotient).
If n = 3k:  , 3k + 2, 3k + 4
, 3k + 2, 3k + 4
If n = 3k+2: 3k+2, 3k + 4, 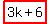
If n = 3k+4: 3k+4, 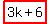 , 3k + 8
, 3k + 8
In each case, one and only one out of n, n+2, n+4 is divisible by 3