Question 619032: Find a polynomial P(x) with real coefficients having a degree 6, leading coefficient 5, and zeros 3,0 (multiplicity 3), and 2-4i.
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! - Polynomials of a certain degree will have that many zeros. Since P(x) is supposed to be of degree 6, P(x) will have 6 zeros.
- Polynomials with real coefficients and complex zeros will always have those zeros in pairs of conjugates. Since P(x) is such a polynomial and since it has a zero of 2-4i, then 3+4i will also be a zero. (This gives us the needed 6th zero.)
- For each zero, there will be a factor of P(x) of the form (x-z) where "z" is the zero. So P(x) will have the following factors:
- (x-3)
- (x-0) (or just x)
- (x-0) (or just x)
- (x-0) (or just x)
- (x-(2-4i) (or (x-2+4i))
- (x-(2+4i) (or (x-2-4i))
- To get a desired leading coefficient, is make it an additional factor.
Putting this all together we have:

Now we just simplify. Since this is all multiplication and since multiplication is commutative (i.e. the order does not matter), we can multiply in any order we choose. With clever use of the  pattern we can make multiplying the factors with the complex numbers relatively easy. With an "a" of "x-2" and a "b" of "4i", (x-2+4i) is (a+b) and (x-2-4i) is (a-b). And from the pattern we know the result of multiplying them is pattern we can make multiplying the factors with the complex numbers relatively easy. With an "a" of "x-2" and a "b" of "4i", (x-2+4i) is (a+b) and (x-2-4i) is (a-b). And from the pattern we know the result of multiplying them is  or, in this case, or, in this case,  We can use the We can use the  pattern to square (x-2) and we can replace pattern to square (x-2) and we can replace  with -1. So with -1. So  . This may not have been easy, but it was much easier this way than any other way. And by multiplying the factors with the i's first, the i's have now disappeared, making the remaining multiplications easier. So now we have: . This may not have been easy, but it was much easier this way than any other way. And by multiplying the factors with the i's first, the i's have now disappeared, making the remaining multiplications easier. So now we have:

Continuing with "easiest first" we'll multiply the x's and the 5:

Using the Distributive Property we can multiply the 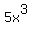 and the (x-3): and the (x-3):

One more multiplication. Multiplying each term of one factor times each term of the other:

Simplifying...


|
|
|