SOLUTION: Show that one and only one out of n, n+2 and n+4 is divisible by 3, where ‘n’ is any positive integer.

Algebra ->  Real-numbers -> SOLUTION: Show that one and only one out of n, n+2 and n+4 is divisible by 3, where ‘n’ is any positive integer.      Log On


   

Question 618978: Show that one and only one out of n, n+2 and n+4 is divisible by 3, where ‘n’ is any positive integer.
Answer by ewatrrr(24785) About Me  (Show Source):
You can put this solution on YOUR website!
 

Hi,

Show that one and only one out of  n, n+2 and n+4 is divisible by 3, where ‘n’ is any positive integer.

By the Division Algorithm, n is either of the form 3k, 3k + 1, or 3k + 2.

3k: highlight%283k%29,3k+2,3k+4

3k+1: 3k+1, 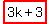highlight%283k%2B3%29, 3k+5

3k+2: 3k+2, +3k+4,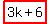highlight%283k%2B6%29

In either of the allowed forms, there is only one of n, n+2 and n+4 divisible by three