SOLUTION: If f(x)= (2x-3)/5 , find f<sup>-1</sup>(x)

Algebra ->  Logarithm Solvers, Trainers and Word Problems -> SOLUTION: If f(x)= (2x-3)/5 , find f<sup>-1</sup>(x)      Log On


   

Question 61871: If f(x)= (2x-3)/5 , find f-1(x)
Answer by Edwin McCravy(20060) About Me  (Show Source):
You can put this solution on YOUR website!
If f(x)= (2x-3)/5 , find f-1(x)

        2x - 3 
f(x) = --------
           5

I want you to also learn the graphical significance of
inverse as we go, so here is the graph of f(x) in red
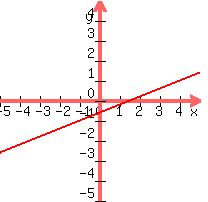+graph%28+200%2C+200%2C+-5%2C+5%2C+-5%2C+5%2C+%282x-3%29%2F5%29+ 
Replace f(x) by y

     2x - 3 
y = --------
        5

Interchange x and y

     2y - 3 
x = --------
        5

Solve for y.

Multiply both sides by 5 to clear of fractions:

5x = 2y - 3

Add 3 to both sides

5x + 3 = 2y

Divide both sides by 2

 5x + 3
-------- = y
    2

or

     5x + 3
y = -------- 
        2
  
Replace y by f-1(x)

          5x + 3
f-1(x) = -------- 
             2

Now look at the graph of f-1(x) in green:
+graph%28+200%2C+200%2C+-5%2C+5%2C+-5%2C+5%2C+0%2C+%285x%2B3%29%2F2%29+
Now look what happens when we place them on the same 
set of axes:
+graph%28+200%2C+200%2C+-5%2C+5%2C+-5%2C+5%2C+%282x-3%29%2F5%2C+%285x%2B3%29%2F2%29+
Now watch what happens when we draw the line y = x
(That's called the identity line, because y and x are 
identically equal in the equation y = x. I'll draw it in
blue:
+graph%28+200%2C+200%2C+-5%2C+5%2C+-5%2C+5%2C+%282x-3%29%2F5%2C+%285x%2B3%29%2F2%2C+x%29+
Notice that the graph of the green line (the inverse) 
is the reflection of the original function's graph,
drawn in red, across the identity line y=x, drawn in
blue.

Edwin