Determine whether each of the distributions given below represents a probability distribution. Justify your answer.
All the probabilities must be
1. All probabilities between 0 and 1 inclusive.
2. The sum of all the probabilities must
equal exactly 1
(A)
x P(x)
1 1/4
2 5/12
3 1/3
4 1/6
1. All those probabilities are between 0 and 1.
2. The sum of the probabilities is
 +
+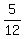 +
+ +
+ =
Get an LCD of 12:
=
Get an LCD of 12:
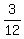 +
+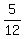 +
+ +
+ =
=
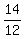 =
=  =
=  No, that sum is not 1, so it is NOT a
probability distribution
(B)
x P(x)
3 0.1
6 3/5
8 0.3
1. All those probabilities are between 0 and 1.
2. The sum of the probabilities is
0.1+
No, that sum is not 1, so it is NOT a
probability distribution
(B)
x P(x)
3 0.1
6 3/5
8 0.3
1. All those probabilities are between 0 and 1.
2. The sum of the probabilities is
0.1+ +0.3 = 0.1+0.6+0.3 = 1.0
Yes, that sum is 1, so it IS a probability
distribution.
(C)
x P(x)
20 0.2
30 -0.2
40 0.7
50 0.3
1. That second probability is negative, and
so it is not a probability distribution.
2. The sum of the probabilities is 1, but
that does not matter. No probability is
ever negative. So it is NOT a probability
distribution.
Edwin
+0.3 = 0.1+0.6+0.3 = 1.0
Yes, that sum is 1, so it IS a probability
distribution.
(C)
x P(x)
20 0.2
30 -0.2
40 0.7
50 0.3
1. That second probability is negative, and
so it is not a probability distribution.
2. The sum of the probabilities is 1, but
that does not matter. No probability is
ever negative. So it is NOT a probability
distribution.
Edwin