Question 618064: How many positive integers have exactly 3 proper divisors, each of which is less than 50? ( A proper divisor of a positive integer n is a positive integer divisor of n other than n itself.)
Found 2 solutions by Edwin McCravy, CarlosOrtiz:
Answer by Edwin McCravy(20056)   (Show Source):
You can put this solution on YOUR website!
There are exactly two kinds of positive integers which have
exactly 3 proper divisors. They are as follows:
1. The cube of a prime p has 3 proper divisors 1, p, and pē.
2. The product of a pair of unique primes p1, p2 has 3 proper
divisors 1, p1, and p2.
There are 15 primes less than 50, which are
2,3,5,7,11,13,17,19,23,29,31,37,41,43,47
The number of cubes of a prime less that 50 is the number of
primes less than 50 which is also 15.
The number of products of a pair of unique primes less than 50
is the number of pairs of primes less than 50 which is 15C2 or
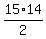 = 105
The total is 15 + 105 or 120.
Edwin
Answer by CarlosOrtiz(1)  (Show Source):
You can put this solution on YOUR website! Answer above is wrong.
true answer:
you have two possible scenarios: p1*p2 = n, n is some number, p1 does not equal p2; and second scenario is p^(3) = n. For all these p's, p < 50. These scenarios are found because both have positive divisor count of 4.
Let's look at the first scenario:
you have, as stated by the other answer, 15 primes that are <50. these primes can be entered into the scenario like so: example: 2*3, 2*5, 2*7 ... 2*p, p<50; 3*5, 3*7, 3*11 ... 3*p, p<50. We can list all of the combinations, or we can realise that as we go down the primes list as in 2, 3, 5, 7, 11, etc. we notice that the possible combinations decreases by 1. For 2*p there are 14 scenarios for primes less than 50 that are not equal to 2 (remember that 2 = p1, and some other number is p2 and p1 does not equal p2. we cannot have 2*2 in this scenario.) So for 2*p, there are 14 different combinations. for 3*p, there are 13 because we already wrote 2*3 in the 2*p scenario, and 3*3 is invalid. The quantity of combinations decreases by one so we have 14, 13, 12 ,11... 1 combinations as we go up the prime count. So we add them up because we are looking for the quantity of integers: (14+6)+(13+7)+(12+8)+(11+9)+(10)+5+4+3+2+1 = 105 positive integers for scenario one.
now for scenario 2 (where we have p^(3)):
notice that we can split p^(3) into p*p^(2) where p is the same value. Then we have numbers like 2*2^(2) and 3*3^(2) and so on. Also, since p^(2) is the larger of the two, we need p^(2) to be <50, and 7^(2) = 49 is the largest prime to be <50. Thus we have p = 2, 3, 5, 7. These are 4 numbers where each cubed is an integer, thus we have 4 additional integers.
from scenario one we got 105 integers that are positive, and from scenario two we got 4 integers.
thus the answer is 105 + 4 = 109.
cheers
Carlos
|
|
|
