_
x - intercepts: ±Ö6
_
y - intercepts: ±2Ö3
Plot those 4 intercepts:
 draw the ellipse
draw the ellipse  Since it looks like this: "
Since it looks like this: " "
and not like this:"
"
and not like this:" ",
its equation is
",
its equation is
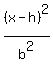 +
+ 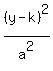 = 1
The center is (h,k) = (0,0), so it has the form
= 1
The center is (h,k) = (0,0), so it has the form
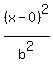 +
+ 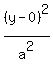 = 1
= 1
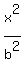 +
+ 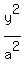 = 1
The y-intercepts are the vertices, the x-intercepts are the covertices:
_
a = semi-major axis = distance between center and a vertex = 2Ö3
Therefore
_
b = semi-minor axis = distance between center and a covertex = Ö6
_ _
Therefore a² = (2Ö3)² = 4·3 = 12, b² = (Ö6)² = 6
= 1
The y-intercepts are the vertices, the x-intercepts are the covertices:
_
a = semi-major axis = distance between center and a vertex = 2Ö3
Therefore
_
b = semi-minor axis = distance between center and a covertex = Ö6
_ _
Therefore a² = (2Ö3)² = 4·3 = 12, b² = (Ö6)² = 6
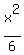 +
+ 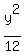 = 1
Edwin
= 1
Edwin