SOLUTION: Use the information provided to write the standard form of the ellipse: Vertices: (-9,3),(-9,-23) Foci: (-9,2), (-9,-22) Please provide a step by step answer.

Algebra ->  Quadratic-relations-and-conic-sections -> SOLUTION: Use the information provided to write the standard form of the ellipse: Vertices: (-9,3),(-9,-23) Foci: (-9,2), (-9,-22) Please provide a step by step answer.      Log On


   

Question 617296: Use the information provided to write the standard form of the ellipse:
Vertices: (-9,3),(-9,-23)
Foci: (-9,2), (-9,-22)
Please provide a step by step answer.
Found 2 solutions by KMST, jsmallt9:
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
STEP 1 - FIGURE OUT WHAT IT LOOKS LIKE:
The vertices are on a horizontal line, with y=-9, so the foci and center are on the same line (in between those vertices).
That line is the major axis, and we say that the ellipse has a horizontal major axis, meaning that is stretched out horizontally (short and fat).

STEP 2 - FIND THE CENTER:
The center of the ellipse is midway between the vertices, so it is the midpoint of the segment between (-9,3), and (-9,-23).
To find the coordinates of the center, you just average the coordinates of the vertices.
%283%2B%28-23%29%29%2F2=-20%2F2=-10 so the center is at (-9,-10).

STEP 3 - FIND THE SEMI-MAJOR AXIS:
That is the distance from the vertices to the center, and it is 13 units:
3-%28-10%29=3%2B10=13 or -10-%28-23%29=-10%2B23=13
We usually call it a, so a=13

STEP 4 - FIND THE FOCAL DISTANCE:
That is the distance from the foci to the center. and it is 12 units:
2-%28-10%29=2%2B10=12 or -10-%28-22%29=-10%2B22=12
We usually call it c, so c=12

STEP 5 - FIND THE SEMI-MINOR AXIS:
That is the distance from the co-vertices to the center.
We usually call it b, and we should know that in an ellipse
a%5E2=b%5E2%2Bc%5E2
Substituting we get
13%5E2=b%5E2%2B12%5E2 --> 169=b%5E2%2B144 --> 169-144=b%5E2 --> b%5E2=25 --> b=5

STEP 6 - WRITE THE EQUATION:
We should know that the standard form of the equation of an ellipse with a horizontal major axis, centered at (h,k) is
%28x-h%29%5E2%2Fa%5E2%2B%28y-k%29%5E2%2Fb%5E2=1
So we substitute the values for h,k,a, and b that we found before and write
%28x-%28-10%29%29%5E2%2F13%5E2%2B%28y-%28-9%29%29%5E2%2F5%5E2=1 --> highlight%28%28x%2B10%29%5E2%2F13%5E2%2B%28y%2B9%29%5E2%2F5%5E2=1%29 or highlight%28%28x%2B10%29%5E2%2F169%2B%28y%2B9%29%5E2%2F25=1%29

NOTE:
You do not need to exactly memorize the formulas.
What you do not remember, you can figure out because it makes sense.
It is easy to see that when you substitute the coordinates of the center,
Take the standard formula for the equation.
If you substitute the coordinates of the center (one at a time), you get vertices and covertices.
They are at distances a and b from the center, and we always choose the largest as a, so that we can calculate c=sqrt%28a%5E2-b%5E2%29 all the time.
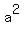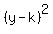The a%5E2%7D%7D+is+under+%7B%7B%7B%28x-h%29%5E2 in the equation when the ellipse extends farther from the center horizontally. (Otherwise, it's under the %28y-k%29%5E2 ).
The formula a%5E2=b%5E2%2Bc%5E2 takes a little more thinking.
The right triangle formed by the center, a focus, and a covertex gives you the formula
a%5E2=b%5E2%2Bc%5E2
The legs of the triangle are b and c.
The hypotenuse is the distance from the focus to the covertex, and we can see that it is a (if someone illuminates the basis for that fact).
The sum of the distances to the foci is the same for all point on an ellipse.
(That's the definition of ellipse, and that should be remembered).
The distance from one vertex to the foci are a-c (for the closest focus) and a+c (for the focus that is far away).
Their sum is (a-c)+(a+c)=2a.
So the sum of the distances form any point on the ellipse to the foci is 2a.
Back to that right triangle whose hypotenuse is the distance from the focus to the covertex.
Because the distance from the covertex to both foci is the same, the sum of the distances from the covertex to both foci (which is 2a) is twice that hypotenuse.

Answer by jsmallt9(3758) About Me  (Show Source):
You can put this solution on YOUR website!
  1. Since the vertices and foci all have the same x coordinates, the major axis must be a vertical line. The standard form for an ellipse with a vertical major axis is:
    %28x-h%29%5E2%2Fb%5E2%2B%28y-k%29%5E2%2Fa%5E2+=+1
  2. The center of the ellipse is halfway between the vertices (or foci). If you cannot "see" what halfway is, then just average the x coordinates and average the y coordinates. These averages will be the x and y coordinates of the center. You should find that the center is:
    (-9, -10)
    The coordinates in the center are represented by the "h" and "k" in the standard form.
  3. The "a" in the standard form is the distance from the center to either vertex. If you cannot "see" what this is, then use the distance formula to find the distance from the center to either vertex. You should get 13 for "a".
  4. The distance from the center to either focus is called "c". ("c" is not in the standard form but we need it to find "b".) Again, if you cannot see what this distance is, use the distance formula. You should find that "c" is 12.
  5. There is an equation that connects a, b and c in an ellipse:
    a%5E2+=+b%5E2+%2B+c%5E2
    Inserting our values for a and c we get:
    13%5E2+=+b%5E2+%2B+12%5E2
    which we can solve for b. Simplifying:
    169+=+b%5E2+%2B+144
    Subtracting 144:
    25+=+b%5E2
    Find the square root. (The a, b and c values are always considered positive numbers so we will ignore the negative square root of 25.)
    5+=+b
  6. We now have the h, k, a and b to fill into our standard form. (See #1):
    %28x-%28-9%29%29%5E2%2F5%5E2%2B%28y-%28-10%29%29%5E2%2F13%5E2+=+1
    which simplifies to:
    %28x%2B9%29%5E2%2F25%2B%28y%2B10%29%5E2%2F169+=+1
P.S. I notice that another tutor has solved this problem, too. But she thinks it is a horizontal ellipse. If you're not sure who is right, then plot the vertices and foci on a graph so see if they line up vertically as I say they do, or horizontally like she says.