Question 617244: ab +bc+ ca , when a + b + c+12 and a*a = b*b +c*c =50
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! I believe you had a typo in your question. Maybe you had to evaluate ab + bc + ca, and were given as information that
a + b + c = 12 and a*a = b*b +c*c =50
(I'll write that last equation as  ) )
If that was the problem, we could start with the product 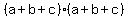
and apply the distributive property twice to get

To simplify the writing, I would like to start omitting some of those asterisks and middle dot symbols for multiplication,
to be able to write 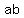 instead of a*b or instead of a*b or  , ,  instead of instead of 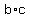 , and the like. , and the like.
I would also apply the commutative property that says that
 , and similarly , and similarly  , and , and  , ,
so that I can write all those products as the ab, bc, or ca in the formula that needs to be evaluated

Next, I would rearrange the terms

I would also group them to get together similar terms.
(I also want to group together the expressions that the problem gives values for).

Now we have that

Next, we replace the known values for 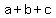 , , 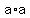 and and 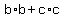
 --> -->  --> --> 
At this point, I first subtract 100 from the expressions on both sides of the equal sign:
 --> -->  --> --> 
Then, I divide the expressions on both sides of the equal sign by 2:
 --> -->  --> --> 

|
|
|