Question 616848: which value of x satisfies the equation cos(3x)=sin60*
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! First of all, Trig functions are periodic. So these equations almost always have an infinite number of solutions. So there will be many. many x's that satisfy your equation.
cos(3x)=sin(60)
First, we should recognize that 60 is a special angle. We should know that sin(60) is  . So we start by replacing sin(60) with its value: . So we start by replacing sin(60) with its value:

The equation now says that a cos equals a number. And this number is a special angle value. For a cos of  the reference angle is the reference angle is  . And since cos is positive in the 1st and 4th quadrant, any angle that terminates in those two quadrants and has a reference angle of . And since cos is positive in the 1st and 4th quadrant, any angle that terminates in those two quadrants and has a reference angle of  will have a cos of will have a cos of 
or

Notes about these equations:- The left side, 3x, is whatever the argument was for cos.
- The "n" on the right sides represents any integer. By replacing "n" with various integers and then adding that to the number in front, you get various angles whose cos's is
 . (Some books.teachers use a lietter different from "n", like "k". The letter used makes no difference. Whatever letter is used, it represents any integer.) . (Some books.teachers use a lietter different from "n", like "k". The letter used makes no difference. Whatever letter is used, it represents any integer.) - The
 and the and the 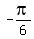 in these equations are specific angles, one for the 1st quadrant and one for the 4th quadrant, whose cos is in these equations are specific angles, one for the 1st quadrant and one for the 4th quadrant, whose cos is  . (Note: Some would use . (Note: Some would use  instead of instead of 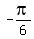 . Either one is fine. They are both 4th quadrant angles with a reference angle of . Either one is fine. They are both 4th quadrant angles with a reference angle of  .) .) - The "+
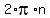 " is a mathematical way of saying "all co-terminal angles". So the first equation says "3x equals all angles that are co-terminal with " is a mathematical way of saying "all co-terminal angles". So the first equation says "3x equals all angles that are co-terminal with  ". The second equation says "3x equals all angles that are co-terminal with ". The second equation says "3x equals all angles that are co-terminal with  ". ". - By using the "n" like this we are able to express the infinite set of solutions to your equation, without having to list them!
Next we solve for x by dividing the equations by 3:

or

(Note how the "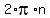 " gets divided by 3, too.) This is what is called the general solution to your equation. " gets divided by 3, too.) This is what is called the general solution to your equation.
Sometimes problems ask for specific solutions, like "find all solutions between 0 and  ". (Yours did not.) When a specific solution is requested, you use the general solution and substitute various integers for "n" until you are satisfied that all the requested solutions have been found. ". (Yours did not.) When a specific solution is requested, you use the general solution and substitute various integers for "n" until you are satisfied that all the requested solutions have been found.
|
|
|