SOLUTION: can you please help solve these problems? much is appriciated. Write a polynomial function f of least degree that has rational coefficients, a leading coefficient of 1, and the gi

Algebra ->  Rational-functions -> SOLUTION: can you please help solve these problems? much is appriciated. Write a polynomial function f of least degree that has rational coefficients, a leading coefficient of 1, and the gi      Log On


   

Question 616663: can you please help solve these problems? much is appriciated.
Write a polynomial function f of least degree that has rational coefficients, a leading coefficient of 1, and the given zeros.

1) -2, -1, 1
2) i, 4
3) i, 2 - √3
4) 1, 4, 1 + √2
Answer by jsmallt9(3758) About Me  (Show Source):
You can put this solution on YOUR website!
Here's a procedure you can follow for this kind of problem:
  1. Determine what our zeros are. This is not as simple as it sounds. For polynomials with rational coefficients, any complex or irrational roots will always occur in conjugate pairs. (More on this later.)
  2. Write the function as a product of factors. Each zero will be represented by a factor. Each factor will be of the form: (x - z) where "z" is a zero of the polynomial
  3. Multiply the factors. (Hint: If there are complex or irrational pairs of zeros, multiply those pairs of factors first.)
I'll do #3 (probably the hardest one) for you and hope that from this procedure and that example, you will be able to figure out the others on your own.

#3. Zeros: i, 2-sqrt%283%29
Step 1. Determine the list of zeros.
i is a complex number so its conjugate will also be a zero. In "a + bi" form i is written as: 0 + 1i. The conjugate is 0 - 1i (or just -i)
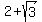
2-sqrt%283%29 is an irrational number (because of the square root). Its conjugate is 2%2Bsqrt%283%29
So the full list of zeros is: i, -i, 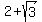2-sqrt%283%29, 2%2Bsqrt%283%29

Step 2: Write the function as a product.
Each of the four zeros gets a factor:

Before we move to step 3, let's simplify the factors a little:
f%28x%29+=+%28x+-+i%29%28x+%2B+i%29%28x+-+2%2Bsqrt%283%29%29%28x+-+2-sqrt%283%29%29

Step 3: Multiply.
As I hinted earlier, it is best to multiply the pairs of factors from the conjugates first. In other "words":


One reason for this hint is that the conjugate pair factors fit the pattern %28a%2Bb%29%28a-b%29+=+a%5E2-b%5E2 This makes multiplying them fast. For example:
%28x-i%29%28x%2Bi%29+=+x%5E2+-+i%5E2
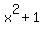
And since i%5E2+=+-1, this becomes: x%5E2%2B1
We can use the pattern on 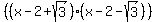%28%28x+-+2%2Bsqrt%283%29%29%28x+-+2-sqrt%283%29%29%29, too, if we look at it in a certain way:
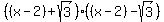
%28%28x+-+2%29%2Bsqrt%283%29%29%28%28x+-+2%29-sqrt%283%29%29%29
Looking at it this way the "a" of the pattern is (x-2) and the "b" is sqrt%283%29. Using the pattern multiply:

which simplifies as follows:


So our function, partially multiplied looks like this:

Now we finish multiplying the last two factors:

This is the polynomial of least degree and rational coefficients that has the given roots.