help Solve the inequality.
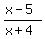 < 1
Subtract 1 from both sides:
< 1
Subtract 1 from both sides:
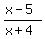 - 1 < 0
- 1 < 0
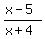 -
-  < 0
Get an LCD of (x+4) and multiply the
< 0
Get an LCD of (x+4) and multiply the  by
by 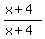 < 0
< 0
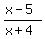 -
-  ·
·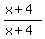 < 0
< 0
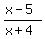 -
- 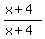 < 0
Combine the numerators over the LCD:
< 0
Combine the numerators over the LCD:
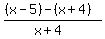 < 0
< 0
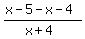 < 0
< 0
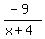 < 0
To find the critical number, set x+4 = 0, getting x = -4
Since there is only one critical number we have only two
intervals to test:
Interval | (-oo,-4) | (-4, oo) |
Test value | -5 | 0 |
Sign of left side | | |
The left side is
< 0
To find the critical number, set x+4 = 0, getting x = -4
Since there is only one critical number we have only two
intervals to test:
Interval | (-oo,-4) | (-4, oo) |
Test value | -5 | 0 |
Sign of left side | | |
The left side is 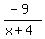 We substitute test value -5 in
We substitute test value -5 in 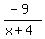
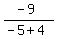 = 9 which is positive so we put a +
Interval | (-∞,-4) | (-4, ∞) |
Test value | -5 | 0 |
Sign of left side | + | |
We substitute test value 0 in
= 9 which is positive so we put a +
Interval | (-∞,-4) | (-4, ∞) |
Test value | -5 | 0 |
Sign of left side | + | |
We substitute test value 0 in 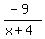
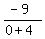 =
= 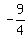 which is negative so we put a -
Interval | (-∞,-4) | (-4, ∞) |
Test value | -5 | 0 |
Sign of left side | + | - |
Since it's < 0 we choose the interval (-4, ∞) as the solution
Edwin
which is negative so we put a -
Interval | (-∞,-4) | (-4, ∞) |
Test value | -5 | 0 |
Sign of left side | + | - |
Since it's < 0 we choose the interval (-4, ∞) as the solution
Edwin