Find all the zeros of
f(x) = x5 - 10x4 + 42x3 -124x2 + 297x - 306
given that one zero is 3i
We will use synthetic division to divide by (x - 3i)
3i | 1 -10 42 -124 297 -306
| +3i -9-30i 90+99i -297-102i 306
1 -10+3i 33-30i -34+99i -102i 0
Now we have factored the polynomial as
f(x) = (x - 3i)[x4 + (-10+3i)x³ + (33-30i)x² - (-102i)x + (-102)]
When a polynomial with all real coefficients has a complex imaginary zero,
its conjugate is also a zero.
Therefore -3i is also a zero
We will use synthetic division to divide
x4 + (-10+3i)x³ + (33-30i)x² - (-102i)x + (-102) by (x - 3i)
-3i | 1 -10+3i 33-30i -34+99i -102i
| -3i 30i -99i -102i
1 -10 33 -34 0
Now we have factored the polynomial as
f(x) = (x - 3i)(x + 3i)(x³ - 10x² + 33x - 34)
We now seek zeros of x³ - 10x² + 33x - 34
The possible rational zeros are ± factors of 34, so they are ±1, ±2, ±17, ± 34
We will use synthetic division to divide by "x - (each of those)" to see if any
are zeros:
We try dividing by x - 1 to see if 1 is a zero:
1 | 1 -10 33 -34
| 1 -9 24
1 -9 24 -10
Nope. We didn't get a remainder of 0.
We try dividing by x + 1 to see if -1 is a zero:
-1 | 1 -10 33 -34
| -1 11 -44
1 -11 44 -78
Nope. We didn't get a remainder of 0.
We try dividing by x - 2 to see if 2 is a zero:
2 | 1 -10 33 -34
| 2 -16 34
1 -8 17 0
We DID get 0 remainder, so now we have factored the
polynomial as
f(x) = (x - 3i)(x + 3i)(x - 2)(x² - 8x + 17)
The last parentheses contains an unfactorable quadratic,
So we use the quadratic formula:
x² - 8x + 17, with a=1, b=-8, c=17
x =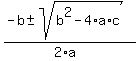 
x = 
x =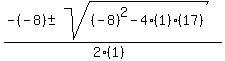 
x = 
x =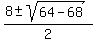 
x = 
x =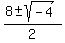 
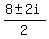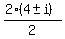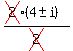x = 4 ± i
So the zeros are 3i, -3i, 2, 4+i, 4-i
Edwin
