Question 616442: please! help me with this => Simplify Remember to use absolute-value notation when necessary. If a root cannot be simplified, state this.
1976 sqrt sign then (2a + b)^1976
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! If your expression is
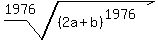
then there is no square root sign. The proper name for what you call a "square root sign" is "radical". Radical symbols are used for all kinds of roots:
Square roots: 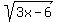 or or 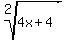
Cube roots: 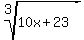
4th roots: 
etc.
Your expression is a 1976th root.
Since 1976 is an even number, a 1976th root is an even-numbered root. Even-numbered roots are not negative. So we must make sure that whatever answer we get, it must not turn out to be negative.
So how do we go about simplifying this? Well, once you understand what roots are, then this problem is extremely easy to simplify. A 1976th root is whatever you have to raise to the 1976th power to get the radicand as a result. ("Radicand" is the name for the expression inside a radical.) So
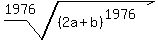
represents whatever you raise to the 1976th power to get 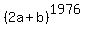 . But can you just see what was raised to the 1976th power to get . But can you just see what was raised to the 1976th power to get 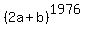 ?? Isn't it simply (2a+b)??? ?? Isn't it simply (2a+b)???
So at first look, 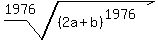 would seem to be 2a+b. would seem to be 2a+b.
But as mentioned earlier, a 1976th root must never be negative. Could 2a+b be negative? Since we don't know what a or b are, we don't know. To ensure the "non-negativeness" of our answer we must use absolute value. So the correct answer is:

P.S. Odd-numbered roots can be any number: positive, negative or zero. So never use absolute value on odd-numbered roots. For example:

P.P.S. You don't always need to use absolute values on even-numbered roots. If you know your answer cannot be negative then the absolute value is not needed. For example:
 (435 is obviously positive. No absolute value needed here.) (435 is obviously positive. No absolute value needed here.)
 (Although we don't know what x might be, we know that (Although we don't know what x might be, we know that  will never be negative. And if will never be negative. And if  cannot be negative, then cannot be negative, then 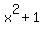 cannot be negative either. So no absolute value is needed.) cannot be negative either. So no absolute value is needed.)
|
|
|