zoe the goat is tied to a rope to one corner of a 15 meter by 25 meter rectangular barn. over what area of the field can zoe graze is the rope is
1. 10 meters long?
2. 20 meters long?
3. 30 meters long?
4. zoe is happiest when she has at least 400 meters squared to graze. what possible lengths of rope could be used?
1. 10 meters long?
 That's 3/4ths of a circle with a radius of 10.
The area of a full circle with radius 10 is
A =
That's 3/4ths of a circle with a radius of 10.
The area of a full circle with radius 10 is
A =  =
=  =
= 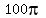 Multiply that by 3/4ths gives
Multiply that by 3/4ths gives  ·
·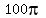 =
= 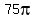 = 235.6 mē
---------------------------------------------
= 235.6 mē
---------------------------------------------
2. 20 meters long?
 That's 3/4ths of a circle with a radius of 20. plus 1/4th of a circle
with a radius of 5
The area of a full circle with radius 20 is
A =
That's 3/4ths of a circle with a radius of 20. plus 1/4th of a circle
with a radius of 5
The area of a full circle with radius 20 is
A =  =
= 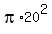 =
= 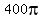 Multiply that by 3/4ths gives
Multiply that by 3/4ths gives  ·
·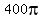 =
= 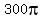 = 942.48 mē
The area of a full circle with radius 5 is
A =
= 942.48 mē
The area of a full circle with radius 5 is
A =  =
= 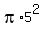 =
=  Multiply that by 1/4th gives
Multiply that by 1/4th gives  ·
· =
= 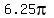 = 19.63 mē
Total area = 942.48+19.63 = 962.11 mē.
-----------------------------------------------------------
= 19.63 mē
Total area = 942.48+19.63 = 962.11 mē.
-----------------------------------------------------------
3. 30 meters long?
 That's 3/4ths of a circle with a radius of 30. plus 1/4th of a circle
with a radius of 15 at the top, plus 1/4 of a circle with radius 5 on
the right.
The area of a full circle with radius 30 is
A =
That's 3/4ths of a circle with a radius of 30. plus 1/4th of a circle
with a radius of 15 at the top, plus 1/4 of a circle with radius 5 on
the right.
The area of a full circle with radius 30 is
A =  =
= 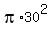 =
= 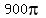 Multiply that by 3/4ths gives
Multiply that by 3/4ths gives  ·
·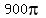 =
= 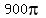 = 2827.43 mē
The area of a full circle with radius 10 is
A =
= 2827.43 mē
The area of a full circle with radius 10 is
A =  =
=  =
= 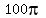 Multiply that by 1/4th gives
Multiply that by 1/4th gives  ·
·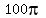 =
=  = 78.54 mē
The area of a full circle with radius 5 is
A =
= 78.54 mē
The area of a full circle with radius 5 is
A =  =
= 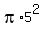 =
=  Multiply that by 1/4th gives
Multiply that by 1/4th gives  ·
· =
= 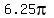 = 19.63 mē
Total area = 2827.43 mē + 78.54 mē + 19.63 mē = 2925.60 mē.
----------------------------------------------------------
= 19.63 mē
Total area = 2827.43 mē + 78.54 mē + 19.63 mē = 2925.60 mē.
----------------------------------------------------------
zoe is happiest when she has at least 400 meters squared to graze. what possible lengths of rope could be used?
To have exactly 400 mē of grazing area, it would be like the first case,
where we just have three-quarters of just one circle. Let the radius
be R.
The area of a full circle with radius R is
A =  Multiply that by 3/4th gives
Multiply that by 3/4th gives  ·
· Setting that = 400
Setting that = 400
 ·
· = 400
Multiply through by 4
= 400
Multiply through by 4
 = 1600
Rē =
= 1600
Rē = 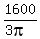 Rē = 169.7652726
R = 13.03 m
So the rope would have to be 13.03 m long or longer.
Edwin
Rē = 169.7652726
R = 13.03 m
So the rope would have to be 13.03 m long or longer.
Edwin