5+5+(5/2)+(2/6)+(5/24)+...
Those denominators are factorials:
4! = 4�3�2�1 = 24
3! = 3�2�1 = 6
2! = 2�1 = 2
1! = 1
also 0! is defined as 1.
Therefore the series:
5 + 5 +  +
+  +
+  + ...
is really
+ ...
is really
 +
+  +
+  +
+  +
+  + ...
which is really:
+ ...
which is really:
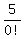 +
+ 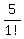 +
+ 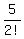 +
+ 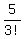 +
+ 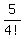 + ... +
+ ... + 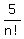 + ...
So, the nth term is
+ ...
So, the nth term is 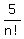 , where we start n with 0.
We put a S in front of that with n=0 on the
bottom and
, where we start n with 0.
We put a S in front of that with n=0 on the
bottom and  on the top, since the ellipsis "..." with
nothing after it indicates that it never ends. So the sigma notation
is
on the top, since the ellipsis "..." with
nothing after it indicates that it never ends. So the sigma notation
is
 By the way, you can use other letters for the "index" (or "dummy variable")
besides n.
These answers are just as good:
By the way, you can use other letters for the "index" (or "dummy variable")
besides n.
These answers are just as good:
 ,
,  ,
,  ,
,  , etc.
You can also start the index (or dummy variable) at 1 by subtracting 1
from the dummy variable after the sigma:
, etc.
You can also start the index (or dummy variable) at 1 by subtracting 1
from the dummy variable after the sigma:
 is the same as
is the same as  In fact you can add any integer to the start of the dummy variable and subtract
the same integer from the dummy variable after the sigma. For instance,
In fact you can add any integer to the start of the dummy variable and subtract
the same integer from the dummy variable after the sigma. For instance,
 is the same as
is the same as  number
Edwin
number
Edwin