SOLUTION: How do you solve 3rē-6r=-3 using the quadratic formula?

Algebra ->  Trigonometry-basics -> SOLUTION: How do you solve 3rē-6r=-3 using the quadratic formula?      Log On


   

Question 616096: How do you solve 3rē-6r=-3 using the quadratic formula?
Answer by fcabanski(1391) About Me  (Show Source):
You can put this solution on YOUR website!
x+=+%28-b+%2B-+sqrt%28+b%5E2-4%2Aa%2Ac+%29%29%2F%282%2Aa%29+


a is the coefficient of the squared element, b is the coefficient of the variable (x or in this case r), and c is the constant.


3r%5E2+-+6r+=+-3 | First move the constant to the left by adding 3 to both sides.


3r%5E2+-+6r+%2B+3+=+0 | Factor out any common factor. In this case it's 3.


{{3{r^2 - 2r + 1 = 0}}} | The removed factor drops because 3 = 0 is never true.


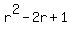r%5E2+-+2r+%2B+1 | Now apply the quadratic formula.


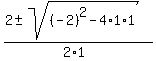%282+%2B-+sqrt%28+%28-2%29%5E2-4%2A1%2A1+%29%29%2F%282%2A1%29+ = %282+%2B-+sqrt%28+4-4+%29%29%2F2+ =


2%2F2+=+1


Contact fcabanski@hotmail.com for online, private tutoring, or personalized problem solving (quick for groups of problems.)