SOLUTION: How do you find the system of equations: x^2+y^2=9 4x^2-4y^2=16

Algebra ->  Quadratic-relations-and-conic-sections -> SOLUTION: How do you find the system of equations: x^2+y^2=9 4x^2-4y^2=16      Log On


   

Question 615654: How do you find the system of equations:
x^2+y^2=9
4x^2-4y^2=16
Answer by jsmallt9(3758) About Me  (Show Source):
You can put this solution on YOUR website!
x%5E2%2By%5E2=9
4x%5E2-4y%5E2=16
As usual, there is more than one way to solve this. One way, which might be the easiest, is to use the Substitution Method. We can quickly solve the first equation for x%5E2 by subtracting y%5E2 from each side:
x%5E2=9-y%5E2
Note: Since the other equation has only an x%5E2 term, we do not have to solve for x, just x%5E2.

Next we substitute the expression we now have for x%5E2 into the other equation:
4%289-y%5E2%29-4y%5E2=16
Distributing the 4 we get:
36+-+4y%5E2-4y%5E2=16
Combining like terms we get:
36+-+8y%5E2=16
Subtracting 36:
-8y%5E2=-20
Dividing by -8:
y%5E2=%28-20%29%2F%28-8%29
Since I'm about to find square roots, I'm only going to reduce the fraction to:
y%5E2=10%2F4
so that I have a perfect square denominator. Now we find the square root of each side. (Remember the negative square roots!)
y+=+sqrt%2810%2F4%29 or y+=+-sqrt%2810%2F4%29
which simplify as follows:
y+=+sqrt%2810%29%2Fsqrt%284%29 or y+=+-sqrt%2810%29%2Fsqrt%284%29
y+=+sqrt%2810%29%2F2 or y+=+-sqrt%2810%29%2F2

We have two y values. So we will have at least two solutions! We can use the "solved for" equation, x%5E2=9-y%5E2, to find the x value(s) for these y values:
For y+=+sqrt%2810%29%2F2:
x%5E2+=+9-%28sqrt%2810%29%2F2%29%5E2
x%5E2+=+9-%2810%2F4%29
x%5E2+=+36%2F4-%2810%2F4%29 Again, keeping the denominator of 4 since a square root is coming)
x%5E2+=+26%2F4
Square root (w/ the negative square roots!):
x+=+sqrt%2826%29%2F2 or x+=+-sqrt%2826%29%2F2
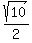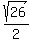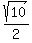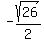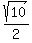For this one y value, sqrt%2810%29%2F2 we get two x values! This means that both (sqrt%2826%29%2F2, sqrt%2810%29%2F2) and (-sqrt%2826%29%2F2, sqrt%2810%29%2F2) are solutions.

For y+=+-sqrt%2810%29%2F2:
x%5E2+=+9-%28-sqrt%2810%29%2F2%29%5E2
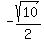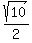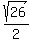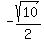I hope you can see that squaring -sqrt%2810%29%2F2 will result in the same thing as squaring sqrt%2810%29%2F2 did above. And since this is true the rest of what follows will be the same as what we did above. So we will end up with the exact same x values, x+=+sqrt%2826%29%2F2 or x+=+-sqrt%2826%29%2F2, for y+=+-sqrt%2810%29%2F2 as we did for y+=+sqrt%2810%29%2F2. So we have two more solutions:
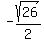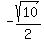(sqrt%2826%29%2F2, -sqrt%2810%29%2F2) and (-sqrt%2826%29%2F2, -sqrt%2810%29%2F2)

All together we have four solutions:
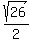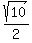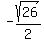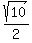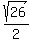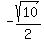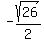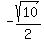(sqrt%2826%29%2F2, sqrt%2810%29%2F2) and (-sqrt%2826%29%2F2, sqrt%2810%29%2F2) and (sqrt%2826%29%2F2, -sqrt%2810%29%2F2) and (-sqrt%2826%29%2F2, -sqrt%2810%29%2F2)

Getting 4 solutions should not be a surprise. The first equation is the equation of a circle centered on the origin. And the second equation is the equation of a hyperbola centered on the origin. If you picture this it should not be hard to imagine that there could be 4 symmetric points of intersection.