SOLUTION: How do you find the equation, center, vertices, and foci of the following problem: 4x^2-16y^2+40x+128y-220=0

Algebra ->  Equations -> SOLUTION: How do you find the equation, center, vertices, and foci of the following problem: 4x^2-16y^2+40x+128y-220=0      Log On


   

Question 615643: How do you find the equation, center, vertices, and foci of the following problem:
4x^2-16y^2+40x+128y-220=0
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
My way:
4x%5E2-16y%5E2%2B40x%2B128y-220=0 --> %284x%5E2%2B40x%29%2B%28-16y%5E2%2B128y%29=220 --> 4%28x%5E2%2B10x%29-16%28y%5E2-8y%29=220
Now, I add a term into each bracket to "complete the square" and (of course) add the same thing to the right side of the equal sign too.
4%28x%5E2%2B10x%29-16%28y%5E2-8y%29=220 --> 4%28x%5E2%2B10x%2B25%29-16%28y%5E2-8y%2B16%29=220%2B4%2A25-16%2A16 --> 4%28x%5E2%2B10x%2B25%29-16%28y%5E2-8y%2B16%29=220%2B100-256 --> 4%28x%5E2%2B10x-25%29-16%28y%5E2-8y%2B16%29=64
Next, I write the brackets as squares:
4%28x%5E2%2B10x%2B25%29-16%28y%5E2-8y%2B16%29=64 --> 4%28x%2B5%29%5E2-16%28y-4%29%5E2=64
Finally, I divide both sides by the value on right side of the equal sign to get the equation in the form I like:
4%28x%2B5%29%5E2-16%28y-4%29%5E2=64 --> 4%28x%2B5%29%5E2%2F64-16%28y-4%29%5E2%2F64=64%2F64 --> %28x%2B5%29%5E2%2F16-%28y-4%29%5E2%2F4=1
Or even better, I can write those denominators as squares, as in:
%28x%2B5%29%5E2%2F4%5E2-%28y-4%29%5E2%2F2%5E2=1
That matches the general equation for a hyperbola with a horizontal transverse axis, centered at (h,k):
%28x-h%29%5E2%2Fa%5E2-%28y-k%29%5E2%2Fb%5E2=1
From that equation, I get the coordinates of the center and the vertices.
The center is (-5,4), from the numbers subtracted from x and y. (You can see that the curve is symmetrical with respect to x=-5 and symmetrical with respect to y=4).
When y=4, %28x%2B5%29%5E2%2F4%5E2=1 --> %28x%2B5%29%5E2=4%5E2 and that is the smallest possible value for %28x%2B5%29%5E2. For all other values of y,
%28x%2B5%29%5E2%2F4%5E2=1%2B%28y-4%29%5E2%2F2%5E2%3E1 and %28x%2B5%29%5E2%3E4%5E2
So abs%28x%2B5%29%3E=4
That is as close to the center as the hyperbola can get, and it gives you the coordinates of the vertices:
%28x%2B5%29%5E2=4%5E2 --> x%2B5=4 or x%2B5=4 --> x=-5+%2B-+4 --> highlight%28x=-9%29 or highlight%28x=-1%29
So the vertices are at (-9,4) and (-1,4).
The foci are on the line conecting the vertices (the transverse axis), at points
at a distance c from the center, with c calculated as
c=sqrt%28a%5E2%2Bb%5E2%29, so c=sqrt%284%5E2%2B2%5E2%29=sqrt%2816%2B4%29=sqrt%2820%29=2sqrt%285%29
So the foci are at (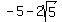-5-2sqrt%285%29,4) and (-5%2B2sqrt%285%29,4).