|
Question 615615: Find the least common multiple 2x^2. 4x. X^3. (x-1). (x-1)^2
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! When finding LCM's it can be helpful to write each expression, fully factored, in a certain way. (By "fully factored" I mean- factor until nothing esle can be factored
- factoring numbers into primes
- if there are exponents on a factor, rewrite them without an exponent
Once you have have each expression fully factored write them in a certain way:
2x^2 = 2 * x * x
4x = 2 * x * 2
x^3 = x * x * x
(x-1) = (x-1)
(x-1)^2 = (x-1) * (x-1)
Note how I used spacing and the fact that order does not matter in multiplication to arrange the factors so that each column has the same factor in it. The first column only has 2's, the second and 3rd columns each have only x's, the 4th column is another column of 2's, the 5th column is a 3rd column of x's, and the 6th and 7th columns are columns for (x-1) factors. By lining up the factors this way the LCM can be found easily. THe LCM is the product of all the columns:
2x^2 = 2 * x * x
4x = 2 * x * 2
x^3 = x * x * x
(x-1) = (x-1)
(x-1)^2 = (x-1) * (x-1)
LCM = 2 * x * x * 2 * x * (x-1) * (x-1) = 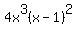
Note how each column contributes only 1 factor to the LCM, no matter how many of that factor there were in the column above! Not only is this a reliable way to find an LCM it can be useful in other ways:- One of the most common uses for LCM's is when you need to add fractions and you are looking for the lowest common denominator. Not only will the above procedure help you find the lowest common denominator, but it will help you figure out how to change each fraction so it has that denominator. Lets say we want to add
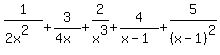
You would go through the procedure above and find that the LCM of the denominators is 2 * x * x * 2 * x * (x-1) * (x-1). Then to change the denominators into 2 * x * x * 2 * x * (x-1) * (x-1) (or 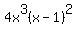 ), we just compare the factored form of each denominator to see what is "missing". Comparing ), we just compare the factored form of each denominator to see what is "missing". Comparing
2x^2 = 2 * x * x
to
LCM = 2 * x * x * 2 * x * (x-1) * (x-1)
we can see that the 2x^2 is "missing": 2 * x * (x-1) * (x-1). So we will multiply the numerator and denominator of the first fraction by 2 * x * (x-1) * (x-1) (or 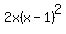 ). You can repeat this for each fraction. Then the denominators will all be the same and you can finally add the fractions. ). You can repeat this for each fraction. Then the denominators will all be the same and you can finally add the fractions. - The above procedure for LCM's can also be used to find greatest common factors, GCF's. For GCF's you only use factors from columns that are "full". IOW, only use factors that are columns without any empty spaces. For example, with
2x^2 = 2 * x * x
4x = 2 * x * 2
x^3 = x * x * x
(x-1) = (x-1)
(x-1)^2 = (x-1) * (x-1)
There are no full columns, Every column is "empty" in at least one row. When this happens the GCF is 1 (since 1 is a factor of everything). A different example:
6x^3(x-3) = 2 * 3 * x * x * x * (x-3)
8x(x-3)^2 = 2 * x * (x-3) * 2 * 2 * (x-3)
GCF = 2 * x
Here the GCF would just be 2 * x (or 2x) since only the first column and the 3rd column are full. FWIW, the LCM for these two would be: 2 * 3 * x * x * x * (x-3) * 2 * 2 * (x-3) (or 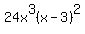 ). ).
|
|
|
| |