SOLUTION: I need help finding the sum or difference,then classifying each polynomial and finding the leading coefficient and degree  . I Just need help solving two questions to give me an id

Algebra ->  Polynomials-and-rational-expressions -> SOLUTION: I need help finding the sum or difference,then classifying each polynomial and finding the leading coefficient and degree  . I Just need help solving two questions to give me an id      Log On


   

Question 615497: I need help finding the sum or difference,then classifying each polynomial and finding the leading coefficient and degree  . I Just need help solving two questions to give me an idea of how to solve it and ill be fine from there
(4x^4+2x^2+1)+(3x^2-8x-1) The other question is (x^9+2x+6)-(2x-7)
Answer by jsmallt9(3758) About Me  (Show Source):
You can put this solution on YOUR website!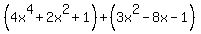
%284x%5E4%2B2x%5E2%2B1%29%2B%283x%5E2-8x-1%29
The key to adding and subtracting polynomials, IMHO, is to change all subtractions into additions. Once the entire expression is made up of additions, you can then use the...
  • Commutative Property to rearrange the order as you choose.; and
  • Associative Property to change the grouping in any way you choose.
The hardest part, which is not especially hard, is to learn how to change subtractions into additions correctly. When a term is being subtracted, like the 8x and the 1 in
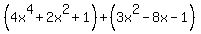
%284x%5E4%2B2x%5E2%2B1%29%2B%283x%5E2-8x-1%29
it is quite easy to change it to addition. Just change the operation to addition and change the subtracted term to its opposite. Changing the the subtractions above we get:
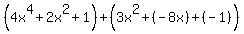
%284x%5E4%2B2x%5E2%2B1%29%2B%283x%5E2%2B%28-8x%29+%2B+%28-1%29%29
Now that everything is addition we can:
  1. Use the Associative Property to remove the grouping:
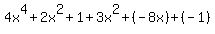    4x%5E4%2B2x%5E2%2B1%2B3x%5E2%2B%28-8x%29+%2B+%28-1%29
  2. Use the Commutative Property to rearrange the order, putting terms in order from highest exponent to lowest:
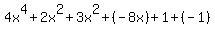    4x%5E4%2B2x%5E2%2B3x%5E2%2B%28-8x%29+%2B+1+%2B+%28-1%29
  3. If there are like terms, use the Associative Property to group them:
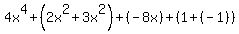    4x%5E4%2B%282x%5E2%2B3x%5E2%29%2B%28-8x%29+%2B+%281+%2B+%28-1%29%29
  4. Simplify:
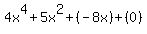
    4x%5E4%2B5x%5E2%2B%28-8x%29+%2B+%280%29
    which simplifies to:
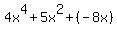
    4x%5E4%2B5x%5E2%2B%28-8x%29
    This is the answer. Although I don't recommend it, you can change any additions of negatives back to subtractions: 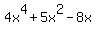4x%5E4%2B5x%5E2-8x

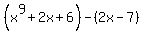
    %28x%5E9%2B2x%2B6%29-%282x-7%29
In your other question we have a subtraction of a term, the 7, and a subtraction of an expression, - (2x-7). This is where changing subtractions to additions can be a little difficult. First we change the subtraction of 7 to an addition:
%28x%5E9%2B2x%2B6%29-%282x%2B+%28-7%29%29
Then we change the subtraction of the expression to an addition. When changing the subtraction of an expression, you change the operation to addition and change every term in the expression to its opposite:
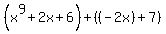
%28x%5E9%2B2x%2B6%29%2B%28%28-2x%29%2B+7%29
Now that everything is addition...
  1. Use the Associative Property to remove the groupings:
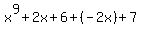    x%5E9%2B2x%2B6%2B%28-2x%29%2B+7
  2. Use the Commutative Property to put the terms in order from highest exponent to lowest:
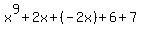    x%5E9%2B2x%2B%28-2x%29%2B6%2B+7
  3. If there are like terms, use the Associative Property to group them:
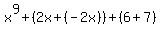    x%5E9%2B%282x%2B%28-2x%29%29%2B%286%2B+7%29
  4. Simplify:
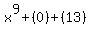
    x%5E9%2B%280%29%2B%2813%29
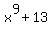
    x%5E9%2B13
Once you get some practice with this, you will be able to do many of these steps in your head.

As for the other issues:
  • Degree. Both terms and expressions have degrees:
    • The degree of a term is the sum of the exponents of its variables. If a term has no variables, its degree is 0. Some examples:
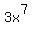      • 3x%5E7 : Degree = 7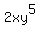
      • 2xy%5E5 : Degree = 1 + 5 = 6
      • 12.3 : Degree = 0
    • The degree of a polynomial is the degree of the term with the highest degree. If the terms are in proper order, from highest exponent to lowest, then the degree of the polynomial is the degree of the first term.
  • Leading coefficient: If you put the terms of the simplified polynomial in order from highest exponent to lowest, the leading coefficient is the first coefficient (the coefficient of the term with the highest degree). In the first polynomial, the leading coefficient is 4 and in the second it is 1.