Question 615399: Find all values of x in the interval 0 degreesis less than or equal to x wich is less than or equal to 360 degrees, that satisfy the equation 3 cos 2x = cos x +2. Express your answer to the nearest degree.
Answer by jsmallt9(3758)   (Show Source):
You can put this solution on YOUR website! 
When solving equations like this you often want all the arguments of the functions to be the same. So we will first look at either changing the argument of 2x into x or the argument of x into 2x. We have a formula for cos(2x) will will convert the argument to x. In fact, there are three variations of the formula:Any of these will work. I am going to use the second formula because not only will it change the argument as planned but the functions will match, too. They will all be cos. Replacing the cos(2x) with the second form we get:
which simplifies to:
Now we solve for cox(x). Since this equation is quadratic form for cox(x) (because of the  ). So we want one side to be a zero. Subtracting cos(x) and 2 from each side we get:
Next we factor:
From the Zero Propduct Property we know that one of the factors must be zero:
6cos(x) + 5 = 0 or cos(x)-1 = 0
Solving these for cos(x) we get:
 or 
Let's look at cos(x) = 1 first. A cos of 1 is a special angle value. We should recognize this and know that only an angle of zero (or an angle co-terminal with zero) will have a cos of 1. For this we write:
For the other equation, , we should recognize that -5/6 is not a special angle value for cos (or for any other function for that matter). So we will need to use a calculator. We will use the cos^(-1) button. When using the the inverse buttons, you rarely enter a negative value. You should enter 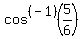 to find the reference angle. If your calculator is set to degree mode and if you enter the above correctly, the calculator should give you a reference angle close to 33.55730976 degrees. Rounded to the nearest degree (as your problem requests), the reference angle is 34 degrees.
Now we use the fact that the cos was negative to determine the quadrants in which x must terminate. Cos is negative in the 2nd and 3rd quadrants. With these quadrants and the reference angle of 34 degrees, we can write the following equations:
 (for the 2nd quadrant)
and
 (for the 3rd quadrant)
These simplify to:
 (for the 2nd quadrant)
and
 (for the 3rd quadrant)
This makes our general solution:
or
From these equations we can find all the x's that are in the interval of 
From
we get x = 0 when n = 0 and we get 360 when n = 1. All other integer values for n result in x's that are too big or too small.
From
we get x = 146 when n = 0. All other integer values for n result in x's that are too big or too small.
From
we get x = 214 when n = 0. All other integer values for n result in x's that are too big or too small.
So the only x's in the interval that are solutions to the equation are: 0, 146, 214 and 360.
|
|
|
