Question 614986: Find all the solutions of the following interval {0, 2π] of 2sin^2 A/2 = 1 + cos^2 A
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
Solving equations like this usually starts with using algebra and/or Trig. properties to transform the equation into one or more equations of the form:
TrigFunction(expression) = number
Making this transformation often (but not always) involves using Trig. properties to change the equation so that the Trig. functions all have the same arguments. Here, we would look to transforming- the A/2 into A. The
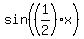 property/formula could be used for this. property/formula could be used for this. - the A into A/2. One of the cos(2x) formulas could be used for this.
- both the A/2 and the A into some third expression. Since we already have found options for the above, we will not pursue this path any further.
I'll show you both of the first two. First, using 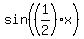 to convert the A/2 to A. (Normally one avoids the half angle formulas because of the plus or minus and because of the square root involved. But here, our sin is squared. So the plus or minus and the square root become non-issues.) to convert the A/2 to A. (Normally one avoids the half angle formulas because of the plus or minus and because of the square root involved. But here, our sin is squared. So the plus or minus and the square root become non-issues.)

which simplifies as follows:


Not only have we matched the arguments, but we have also matched the functions. This is good progress.
Now we solve for cos(A). Since this is a quadratic equation we want one side to be zero. Subtracting 1 and adding cos(A) to each side we get:

Now we factor out the GCF:
0 = cos(A)(cos(A) + 1)
Using the Zero Product Property:
cos(A) = 0 or cos(A) + 1 = 0
Solving the second one:
cos(A) = 0 or cos(A) = - 1
We now have transformed the original equation into two equations of the desired form.
Next we write the general solution. Since cos values of 0 and -1 are both special angle values we should not be using a calculator for this:
For cos(A) = 0:

or

For cos(A) = -1:

All three of these are the general solution. All three, for various integer values for "n", will generate values for A that fit your equation.
NOTES:- Trig functions are periodic. So equations like this like usually have an infinite number of solutions. In this case, all the angles whose cos is 0 or -1 are solutions.
- Fortunately we don't have to try to list an infinite set of solutions. The
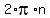 in these equations is how these infinite solutions can be expressed. The "n" can be assigned any integer value. And for each of these values a certain value for A will result. And since there are an infinite number of integers for "n", an infinite number of A's can be expressed. in these equations is how these infinite solutions can be expressed. The "n" can be assigned any integer value. And for each of these values a certain value for A will result. And since there are an infinite number of integers for "n", an infinite number of A's can be expressed. - Some books/teachers do not use "n". They use another letter, like "k". The letter used is not important. What's important is that the letter represents integers.
- The
 in in  represents a full period. This, combined with integer value for "n" expresses the idea of all the co-terminal angles. For example: represents a full period. This, combined with integer value for "n" expresses the idea of all the co-terminal angles. For example:

tells us that A can be  or any angle co-terminal with or any angle co-terminal with  . .
From the general solution we find specific solutions. Many problems, like yours, asks for specific solutions like "find the smallest positive solution" or "find all solutions within the interval...". Your problem asks for solutions within an interval.
To find specific solutions, just try different integers for "n" in the general solution equations until you are comfortable you have found the desired specific solution(s).
We'll start with the general solution equation:

Trying n = 0 in this equation we get A =  . This is in the interval so this is one of the specific solutions. Trying positive integers for n result in A's that are larger than . This is in the interval so this is one of the specific solutions. Trying positive integers for n result in A's that are larger than  and trying negative n's will result in A's that are negative (i.e. less than 0). So we get only one specific solution from this equation. and trying negative n's will result in A's that are negative (i.e. less than 0). So we get only one specific solution from this equation.
Next we try

Again, n = 0 gives us a solution within the interval,  . And positive n's give us A's too large and negative n's gives us A's that are too small. . And positive n's give us A's too large and negative n's gives us A's that are too small.
Next we try

Again, n = 0 gives us a solution within the interval,  . And positive n's give us A's too large and negative n's gives us A's that are too small. . And positive n's give us A's too large and negative n's gives us A's that are too small.
NOTE: Although we seem to have a pattern here do not expect that:- n = 0 will always give you a solution that you want
positive n's make solutions that are too large and negative n's make solutions that are too small.- there will only be one specific solution from each general solution equation. Sometimes there will be more than one; sometimes there will be no specific solutions.
So the only specific solutions within the desired interval are:  , ,  and and  . .
As promised, I am also going to show you how to turn the argument of A into an argument of A/2 using the cos(2x) formula.

There are three variations of the cos(2x) formula. They will all work. But, since the left side has sin, I am going to use the 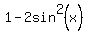 variation so that not only will both arguments be A/2, but both functions will be sin: variation so that not only will both arguments be A/2, but both functions will be sin:

which simplifies as follows:


Solving the rest of this is quite difficult. I wanted to show this because in hopes that- You might learn how to use the various formulas more powerfully. Many student don't realize that the cos(2x) formula can be used to, in effect, divide an argument in two like we did here.
- You might learn that there are usually options. And so if you run into an overly complex situation, like
 , that you would then decide to start again and pursue a different path. With this problem, the , that you would then decide to start again and pursue a different path. With this problem, the 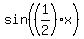 which is usually a bit of a pain to work with, turns out to be the easy path. which is usually a bit of a pain to work with, turns out to be the easy path.
In case you're curious...
Subtracting 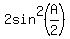 from each side: from each side:

Dividing both sides by 2:

Factoring:


Using the Zero Product Property:
 or or  or or 
Solving:
 or or  or or 
 or or  or or 
 or or  or or 
Remembering both the positive and negative square roots, and since 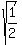 rationalizes to rationalizes to  we get: we get:
 or or  or or  or or 
These are all special angle values for sin. The general solution equations:
For  : :

or

For  : :

or

For  : :

For  : :

Now we solve these for A by multiplying by 2:

or

or

or

or

or

(Note how the 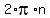 's also get multiplied by 2!) Although this general solution looks very different from the one we got earlier, it is correct, too. It will generate exactly the same A's that the earlier general solution will. And it will generate the exact same specific solutions: 's also get multiplied by 2!) Although this general solution looks very different from the one we got earlier, it is correct, too. It will generate exactly the same A's that the earlier general solution will. And it will generate the exact same specific solutions:
When n = 0 in  we get we get 
When n = 0 in  we get we get 
When n = 0 in  we get we get 
And the other equations, although they are correct, will not give us any solutions that are between 0 and  . .
|
|
|