|
Question 614983: A solid body has a cross-section which is in the shape of the region between the curves  and and  . .
Using calculus, accurately calculate the area under the two curves, between the intersect points.
I plotted my graph and know that it need integrating but not sure how you would do both accurately...add the areas...subtract them? im abit lost
Found 2 solutions by Theo, Alan3354:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! if you graph these curves, you will see that the region is between them as shown below:
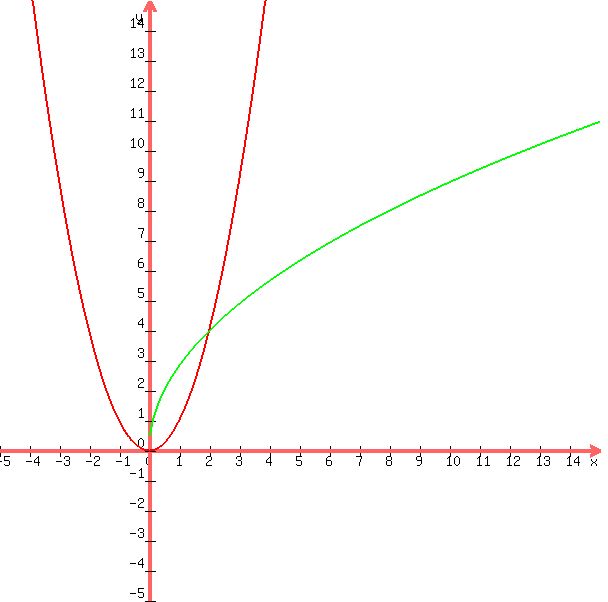
the interval is the value of x from 0 to 2.
you would integrate both equations and you would then take the integral from x = 0 to x = 2 of both equations and subtract the value of the lower equation on the graph from the higher equation on the graph.
in that interval, the higher equation is y = sqrt(8x) while the lower equation is y = x^2
so it would be the integral of sqrt(8x) - the integral of x^2 in the interval from x = 0 to x = 2.
that's my take on it.
i'm very rusty in calculus and don't know much more than that, but that's my best guess for your problem.
essentially, the area for the higher curve is between the x-axis and that curve.
the area for the lower curve is between the x-axis and that curve.
when you subtract the area of the lower curve from the area of the upper curve, you are taking the area that is between them and nothing else.
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! A solid body has a cross-section which is in the shape of the region between the curves  and and  . .
Using calculus, accurately calculate the area under the two curves, between the intersect points.
---------------
Area between = Area under y = sqrt(8x) - area under y = x^2 bounded by the x-axis from x = 0 to 2.
-----------
INT(8x)^(1/2) = (8x)^(3/2)*(2/3)/8 = ((8x)^1.5)/12
@ x=2 --> 16/3 sq units
------------
INT(x^2) = (x^3)/3
@x = 2 --> 8/3
==============
--> Area between = 8/3 sq units
|
|
|
| |