|
Question 614971: A tunnel through a mountain for a four lane highway is to have a semi-
elliptical opening. The total width of the highway is 48 ft and the height at
the edge of the road must be sufficient for a truck 11 ft high to clear. If
the highest point of the opening is to be 15 ft, approximately how wide must
the opening be?
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
You can put this solution on YOUR website! A tunnel through a mountain for a four lane highway is to have a semi-
elliptical opening. The total width of the highway is 48 ft and the height at
the edge of the road must be sufficient for a truck 11 ft high to clear. If
the highest point of the opening is to be 15 ft, approximately how wide must
the opening be?
 The semi-ellipse must be as above. We put the center at the origin. Since the
height is 15 feet, the semi-minor axis = b = 15.
The total width of the highway is 48 feet, so each lane must be 24 feet wide.
For a truck 11 feet high to just scrape the top of the tunnel, when its
right side is at the edge of the highway, the ellipse must pass through the
point (24,11), and also the point (-24,11).
[Note: It would be more practical to make to make it 1 foot higher, to go
through (24,12) instead of (24,11) so that an 11-foot tall truck would have a
1-foot clearance and not scrape the top, but the problem didn't state any
clearance, so I will let the truck scrape the top at the edge of the highway]
The equation of an ellipse is
The semi-ellipse must be as above. We put the center at the origin. Since the
height is 15 feet, the semi-minor axis = b = 15.
The total width of the highway is 48 feet, so each lane must be 24 feet wide.
For a truck 11 feet high to just scrape the top of the tunnel, when its
right side is at the edge of the highway, the ellipse must pass through the
point (24,11), and also the point (-24,11).
[Note: It would be more practical to make to make it 1 foot higher, to go
through (24,12) instead of (24,11) so that an 11-foot tall truck would have a
1-foot clearance and not scrape the top, but the problem didn't state any
clearance, so I will let the truck scrape the top at the edge of the highway]
The equation of an ellipse is
 + +  = 1
But since the center is (h,k) = (0,0), the equation simplifies to = 1
But since the center is (h,k) = (0,0), the equation simplifies to
 + +  = 1
We know that b = 15, so we have = 1
We know that b = 15, so we have
 + +  = 1 = 1
 + +  = 1
Since it goes through the point (24,11), we substitute (x,y) = (24,11) = 1
Since it goes through the point (24,11), we substitute (x,y) = (24,11)
 + + 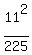 = 1 = 1
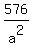 + + 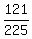 = 1
Solve that for "a" and get
a = 35.30090432, the semi-major axis.
The width of the opening must be the entire major axis,
so the answer to your problem is twice that or 70.60180865 feet.
Edwin = 1
Solve that for "a" and get
a = 35.30090432, the semi-major axis.
The width of the opening must be the entire major axis,
so the answer to your problem is twice that or 70.60180865 feet.
Edwin
|
|
|
| |