Question 614924: HOW MANY SUBSETS ARE POSSIBLE FROM A SET WITH 55 ELEMENTS?
Found 3 solutions by solver91311, ashipm01, Theo:
Answer by solver91311(24713)   (Show Source):
Answer by ashipm01(26)  (Show Source):
You can put this solution on YOUR website! There are  subsets of an n element set. So, for n = 55, as in the problem statement, there are 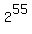 , or 36,028,797,018,963,968, subsets.
The reason there are subsets is because each of the n elements in the set will either be in each subset or it will not be. So for each of the n elements, there are two possible states each one can be in for each subset, and thus there are ways of forming subsets from an n element set.
Take for example this set of three elements: {1, 2, 3}. Since there are three elements, there are  subsets, shown here.
{},
{1},
{2},
{3},
{1,2},
{1,3},
{2,3},
{1,2,3}
The first subset is the empty set. That is formed by not including any of the elements. Next is just a single element subset formed by including the first element and excluding the other two elements. Each of the remaining subsets is formed in a similar manner, by including some elements and excluding other elements. And for each element, it is either in or out of each subset, so there are subsets for any n element set.
Answer by Theo(13342)  (Show Source):
You can put this solution on YOUR website! how many subsets are possible in a set with 3 elements.
let's see.
suppose the elements are a,b,c
you can have:
abc
ab
ac
bc
a
b
c
how many subsets are possible in a set with 4 elements.
let's see.
suppose the elements are a,b,c,d
you can have:
abcd
abc
abd
acd
bcd
ab
ac
ad
bc
bd
cd
a
b
c
d
we don't count the null set (no elements in it).
the number of subsets when you have 3 elements becomes:
3c1 + 3c2 + cc3
the number of subsets when you have 4 elements becomes:
4c1 + 4c2 + 4c3 + 4c4
the number of subsets when you have 55 elements becomes:
55c1 + 55c2 + 55c3 + ......... + 55c54 + 55c55
that's a big number.
i used excel to calculate it.
here's the results:
total >>>>>>>>>>>> 3.60288E+16
n x ncx
55 1 55
55 2 1485
55 3 26235
55 4 341055
55 5 3478761
55 6 28989675
55 7 202927725
55 8 1217566350
55 9 6358402050
55 10 29248649430
55 11 1.19654E+11
55 12 4.3873E+11
55 13 1.45118E+12
55 14 4.35355E+12
55 15 1.18997E+13
55 16 2.97493E+13
55 17 6.82483E+13
55 18 1.4408E+14
55 19 2.80576E+14
55 20 5.05037E+14
55 21 8.41729E+14
55 22 1.30085E+15
55 23 1.86644E+15
55 24 2.48859E+15
55 25 3.08585E+15
55 26 3.5606E+15
55 27 3.82435E+15
55 28 3.82435E+15
55 29 3.5606E+15
55 30 3.08585E+15
55 31 2.48859E+15
55 32 1.86644E+15
55 33 1.30085E+15
55 34 8.41729E+14
55 35 5.05037E+14
55 36 2.80576E+14
55 37 1.4408E+14
55 38 6.82483E+13
55 39 2.97493E+13
55 40 1.18997E+13
55 41 4.35355E+12
55 42 1.45118E+12
55 43 4.3873E+11
55 44 1.19654E+11
55 45 29248649430
55 46 6358402050
55 47 1217566350
55 48 202927725
55 49 28989675
55 50 3478761
55 51 341055
55 52 26235
55 53 1485
55 54 55
55 55 1
the total number of possible subsets looks like it's 3.60288 * 10^16.
Each one of the subsets is unique in that it contains at least 1 element in it that's unique from any other subset with the same number of elements in it.
i won't swear that this is correct, but it's based on a reasonable assumption.
look at the set with 3 elements in it and you'll see that each of the subsets is unique.
the subset with 3 elements in it is abc which is the set itself.
every set is a subset of itself.
the subsets with 2 elements in them are unique.
they contain:
ab
ac
bc
the subsets with 1 element in them are unique.
they contain:
a
b
c
we cover all of the subsets by including all subsets that have 1 less element in them then the previous set of subsets.
this is my guess.
like i say, i won't swear to it, but i think it's a reasonable assumption.
without any precedence to guide me, i'd say this is my best guess.
there are intersections with the other subsets.
for example:
the set ab and the set ac have a common element of a.
the set ac and the set bc have a common element of c.
this is to be expected.
they are still unique subsets because they each have an element in them that is not in the other set.
|
|
|
